[科普中国]-牛顿-柯特斯公式

在数值分析上，梯形法则和辛普森法则均是数值积分的方法。它们都是计算定积分的。

这两种方法都属于牛顿-柯特斯公式。它们以函数于等距n+1点的值，取得一个n次的多项式来近似原来的函数，再行求积。

梯形法则梯形法则是：

这等同将被积函数近似为直线函数，被积的部分近似为梯形。1

要求得较准确的数值，可以将要求积的区间分成多个小区间，再个别估计，即：

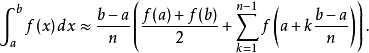
可改写成

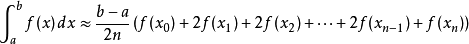
其中对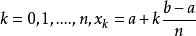

辛普森法则辛普森法则（Simpson's rule，又称森逊法则、辛普森法则）是：

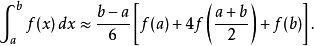
同样地，辛普森法则也有多重的版本：

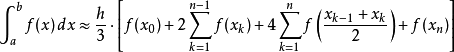
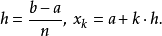
或写成

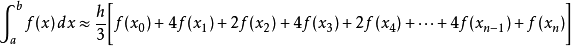
牛顿-柯特斯公式牛顿-柯特斯公式（Newton-Cotes rule / Newton-Cotes formula）以Roger Cotes和艾萨克·牛顿命名。其内容是：

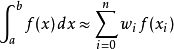
其中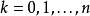 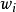， 是常数（由 的值决定）， 。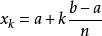

梯形法则和辛普森法则便是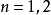 的情况。

亦有不采用在边界点来估计的版本，即取 。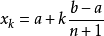

原理假设已知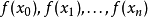的值。

以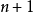点进行插值，求得对应的拉格朗日多项式。

对该次的多项式求积。

该积分便可以作为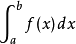的近似，而由于该拉格朗日多项式的系数都是常数（由决定其值），所以积函数的系数（即）都是常数。

缺点对于次数较高的多项式而有很大误差（龙格现象），不如高斯积分法。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学