极限比较审敛法是判别级数敛散性的一种方法。
描述假设存在两个级数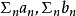 ,且对于任意n都有
,且对于任意n都有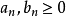 。1
。1
如果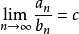 (
(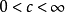 ),那么两级数同时收敛或发散。
),那么两级数同时收敛或发散。
证明对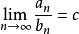 ,我们知道对于任意
,我们知道对于任意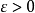 都存在一正整数
都存在一正整数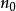 使得当
使得当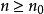 时有
时有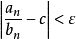 ,等价于
,等价于
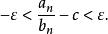
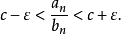
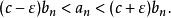 由于c>0,我们可以让
由于c>0,我们可以让 足够小使得
足够小使得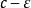 为正。 因此
为正。 因此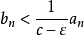 ,根据比较审敛法,如果
,根据比较审敛法,如果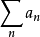 收敛,则
收敛,则 同样收敛。
同样收敛。
类似地,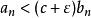 ,如果
,如果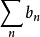 收敛,根据比较审敛法,
收敛,根据比较审敛法,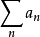 亦收敛。
亦收敛。
因此二者同时收敛或发散。2
例子判断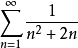 是否收敛。我们将其与收敛级数
是否收敛。我们将其与收敛级数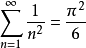 进行比较。
进行比较。
由于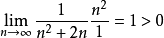 ,我们可以得出原级数收敛。
,我们可以得出原级数收敛。
参见审敛法
比较审敛法
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国