[科普中国]-外尔斯特拉斯逼近定理

魏尔斯特拉斯逼近定理有两个：（1）闭区间上的连续函数可用多项式级数一致逼近。（2）闭区间上周期为2π的连续函数可用三角函数级数一致逼近。

介绍魏尔斯特拉斯逼近定理有两个：

闭区间上的连续函数可用多项式级数一致逼近。

闭区间上周期为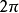的连续函数可用三角函数级数一致逼近。

证明第一逼近定理可以从第二逼近定理直接推出。1

第二逼近定理的证明；

设f(t)为周期为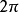的连续函数，定义为一三角级数。

首先证明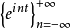，为一个正交函数系：

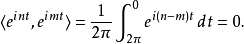
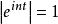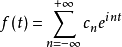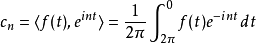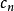(因为)。 故令，于是我们可以求出。 将代入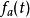的定义式中，有：

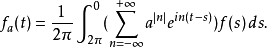
下面对积分号中的和式S求和，令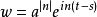，那么就有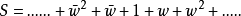：，分成正负两部分求和，可知:

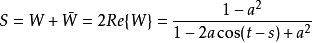带回原积分，有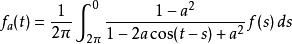，这就是f(s)的泊松积分。其中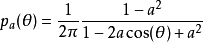称为泊松核。故有：

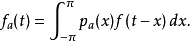我们要检验的的是在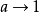时的情况，可以证明：

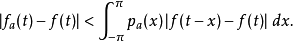
由f(t)的一致连续性，可以证明，上式在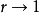时，满足一致收敛的条件，故我们可以用来一致逼近f(t)。

参阅傅里叶级数

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学