[科普中国]-多解析度分析

多解析度分析（multiresolution analysis, MRA）或是多尺度近似（multiscale approximation, MSA）是最常用来分析离散小波转换〈DWT〉或是验证快速小波转换〈FWT〉理论的方法。

简介多解析度分析（multiresolution analysis, MRA）或是多尺度近似（multiscale approximation, MSA）是最常用来分析离散小波转换〈DWT〉或是验证快速小波转换〈FWT〉理论的方法。

本分析方法在1989年及1998年由Stephane Mallat 著作的论文提到。

取样定理取样定理主要是在重建一个时间长度T中被取样过的信号：

若信号是有限带宽，只要奈奎斯特频率（Nyquist frequency）比1/ T小及可完整重建信号；否则得到的重建信号为近似的信号。

因此可以说，愈小的T使得信号的重建愈容易，T的大小将决定信号分辨率，同时，取样频率也受到T的限制。

概念倘若一个信号具有变化速度差异大的区段，像是信号快速变化的区段穿插著变化平缓的区段，则上述单一分辨率将不适用于分析信号。

因此，多解析度分析的概念因此而生。即将信号在不同分辨率上分析。

定义令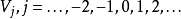为在函数空间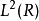里的子空间的数列，

假如

1)分簇性(nested)：

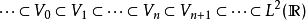
2)稠密性(density)：

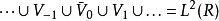
3)分离性(seperation)：

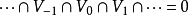
4)调节性(scaling)：

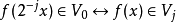
5)正规正交基底(orthonormal basis)：

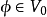且集合为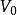的一正规正交基底。

则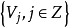为带有调整函数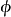的多解析度分析1。

应用在高频的时候，使用较细致的时间分辨率及较粗糙的频率分辨率。

在低频的时候，使用较细致的频率分辨率及较粗糙得时间分辨率。

相当适合使用在长时间都是低频成分，只有在短时间内会有高频成分的信号

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学