[科普中国]-么半范畴

幺半范畴（monoidal category），或称张量范畴（tensor category）， 直觉地讲，是个配上张量积的阿贝尔范畴（abelian category），可当作环的范畴化。

定义数学中中，一个张量范畴（tensor category，或称幺半范畴monoidal category）是一个包含单一个对象的双范畴）bicategory）。

更具体的描述：一个张量范畴是

1）一个范畴 ;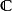

2）被赋予张量积，即一个二元函子

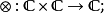
3）被赋予一个单位对象

4）被赋予三组自然同构映射：

结合子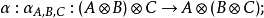

左/右单位子: 自然同构映射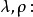

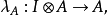
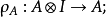
严格幺半范畴严格幺半范畴(strict monoidal category) 是个幺半范畴 ，其自然态射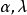 和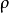 都是恒等影射1。

取任一 范畴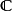 , 我们可构筑其自由严格幺半范畴 ：

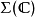1）对象：其每一对象是一串由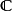 里面的对象组成之有限序列 ；

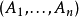2）态射：当且仅当n=m时，我们在二个对象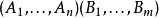 之间定义态射：

每态射 是一串由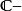态射组成的有限序列 ；

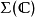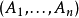3）张量积： 二个-对象及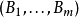之张量积， 我们定义为 此二有限序列之串接 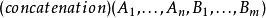； 同样地任何二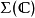-态射之张量积， 我们定义为其串接。

例子取任一范畴，若以其平常范畴积作张量积，以其终对象作单位对象，则成为一个张量范畴。

亦可取任一范畴，以其余积（co-product）作张量积，以其始对象作单位对象，亦成一个张量范畴。 （此二例实为对称幺半范畴结构。） 但亦有许多张量范畴，其张量积 既非 范畴积 亦非 范畴余积。

相关的结构很多张量范畴更进一步有辫,交换态射or封闭等结构。

幺半函子为二张量范畴（么半范畴）间、保存张量积结构之函子；幺半态射为二么半函子间之态射（自然变换 (natural transformations)）。

一般幺半群之概念可推广成么半范畴中的幺半对象。尤其者，可视一严格么半范畴作 范畴之“范畴”Cat中的么半对象（并以卡氏积为么半结构）。

上有界交半格构成一严格对称么半范畴：其积为交，而单位元则为顶。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学