[科普中国]-可去奇点

在复分析中，一个全纯函数的可去奇点（removable singularity），有时称为装饰性奇点（cosmetic singularity）是这样的点，在此处函数表面上没有定义，但是通过细致地分析，函数的定义域可以扩大到该奇点，使得延拓后的函数仍然全纯。

例子例如函数：

对z≠ 0 有一个奇点z= 0。借由定义f(0)=1，可将此奇点消去，并得到全纯的sinc函数。

确切地，如果U是复平面C的一个开集，a是U中一点，f:U- {a} →C是一个全纯函数，如果存在一个在U- {a} 与f相等的全纯函数g:U→C，则a称为f的一个可去奇点。如果这样的g存在，我们说f在a是可全纯延拓的。

黎曼定理黎曼关于可去奇点的定理指出了何时一个奇点是可去的：

定理下列情形是等价的：

i)f可全纯延拓到a。

ii)f可连续延拓到a。

iii) 存在a的一个邻域，在它上面f有界。

iv) limz→a(z - a)f(z) = 0.

蕴含关系 i) ⇒ ii) ⇒ iii) ⇒ iv) 是平凡的。为了证明 iv) ⇒ i)，我们首先回忆到一个函数在a的全纯性等价于解析，即有一个幂级数表示。定义

则

这里由假设(z - a)f(z)可以视为一个D上的连续函数。换句话说，h在D上全纯从而有在a的泰勒级数：

所以

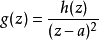是f在a的全纯延拓，这就证明了先前的断言。

其它类型奇点不像实变量函数，1全纯函数有足够的刚性使得其孤立奇点可完全分类。一个全纯函数的奇点要么其实不是真正的奇点，即可去奇点，要么是如下两类居其一：

受黎曼定理启示，给定一个不可去奇点，我们可能问是否存在一个自然数m使得 limz→a(z - a)f(z) = 0。如果存在，a称为f的一个极点，这样最小的m称为a的阶数。所以可去奇点恰好是零阶极点。一个全纯函数在极点附近一致发散到无穷远点。

如果f的一个孤立奇点a既非可去奇点也非极点，则称本性奇点。皮卡定理指出f将任意穿孔开邻域U- {a} 映满整个复平面，至多少一个可能的例外点。

参见解析容量（Analytic capacity）

可去不连续点（Removable discontinuity）

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学