[科普中国]-相容关系

相容关系(Consistent Relation)是一种重要的二元关系，指集合A上具有自反性与对称性的二元关系。若R是A上的相容关系，S⊆A，S内任何两元素有关系R，而A-S内任何元素至少与S内某一个元素没有关系R，则称S是A关于R的一个极大相容类，S的子集都称为相容类。A的任何一个元素组成的单元集都是一个相容类。任何两个元素a，b只要aRb，就组成相容类{a，b}。一般地，任何α个元素，只要在关系图中每两个元素都有双向箭头相连，就组成一个相容类，极大相容类是A的具有这个性质的最大子集，A的极大相容类可以不只一个。A的极大相容类可以不只一个1。

基本介绍定义1 设R是集合A上的一个二元关系，如果R是自反的、对称的，则称R 是相容关系2。

容易看到，等价关系是一种特殊的相容关系，即具有传递性的相容关系。在人际关系中，朋友关系是相容关系，但它不是等价关系，因为它满足自反性、对称性但不满足传递性。

又如，设A是由一些英文单词为元素组成的集合，A={dog,cat,deer,rat,coat,door}, R是A上的二元关系，其定义为:当两个单词具有相同的字母，则认为它们是相关的。

显然，R是自反的、对称的，所以R是相容关系。但R不是等价关系， 因为它不是可传递的，如∈R, ∈R，但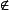 R。

在相容关系的关系图上，每个结点处都有自回路且每两个相关结点间的弧线都是成对出现的。为了简化图形，我们对相容关系图，不画自回路，并且用单线代替成对的弧线。

定义2 设R是集合A上的一个相容关系，C是A的子集，如果对于C中任意两个元素x,y,有∈R，称C是相容关系R产生的相容类。

例如上例的相容关系R,可产生相容类{dog,deer}, {cat, rat, coat}, {door}等 。

对于相容类{dog,deer}， 能加进新的元素组成新的相容类，而相容类{cat,rat,coat}加入任意一个新元素，就不能组成相容类，这里称作最大相容类。

定义3 设R是集合A上的一个相容关系，不能真包含在任何其他相容类中的相容类，称作最大相容类，记作CR。

又如，设A={134，345，275，347， 348，129}， R是A上的二元关系，其定义为: a, b∈A, 且a和b至少有一一个数字相同，则a和b相关。显然R是相容的。A的子集: {134， 347， 348}， {275， 345}， {134， 129}等都是相容类。

对于前两个相容类，都能添加新的元素组成新的相容类。如在相容类{134,347,348}中添加元素: 345， 可组成新的相容类: {134， 345， 347, 348};在相容类(275，345}中添加新的元素: 347，可组成新的相容类: {275， 345，347}。因此相容类{134，347， 348}， {275，345}不是最大相容类。

而对于相容类{129，134}， 添加任意的元素就不再组成相容类，因此相容类{129，134} 是最大相容类。

对于最大相容类也可以认为: R是A上的相容关系，B是相容类，在差集A-B中没有元素能和B中所有元素都相关的，则称B为最大相容类。

在相容关系图中，完全多边形的结点集合，就是相容类。完全多边形是指每个结点与其他结点联接的多边形。例如一个三角形是完全多边形，一个四边形加上两条对角线就是完全多边形。最大完全多边形的结点集合，就是最大相容类。

此外，在相容关系图中，一个孤立结点，以及不是完全多边形的两个结点的连线，也是最大相容类2。

例题解析例1 设给定相容关系图如图1所示，写出最大相容类。

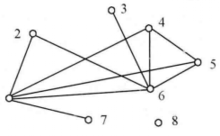
解 最大相容类为: {1, 2，6}，{1, 4, 5，6}， {1， 7}， {3，6}，{8}2。

相关定理定理 设R是有限集A上的相容关系，C是一个相容类，那么一定存在一个最大相容类CR，使得C⊆CR。

证明

设A={a₁，a₂， .. an},构造相容类序列

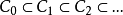其中C0=C ,且 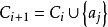，其中j是满足 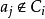而aj与Ci中各元素都有相容关系，且j是满足上述条件的最小下标。

由于A的元素个数|A|=n,所以至多经过n-|C|步，就使这个过程结束，而这个序列的最后一个相容类，就是所要找的最大相容类2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学