[科普中国]-消失动量

消失动量（Vanishing Moments），在连续小波变换（Continuous Wavelet Transform），是一项非常重要的参数，用来检视母小波（Mother wavelet）是否为高频的函数。

消失动量(Vanishing Moments)，在连续小波变换(Continuous Wavelet Transform)，是一项非常重要的参数，用来检视母小波(Mother wavelet)是否为高频的函数。

由来在连续小波变换中，母小波有4个主要限制如下。

1. 有值区间必须是有限的(Compact Support)：

母小波不能是一个无限长的函数。

2. 必须是实函数(Real)：

因为要处理的影像不会是复数信号，且为了方便计算。

3. 偶对称(Even Symmetric)或是奇对称(Odd Symmetric)

4. 消失动量越高越好：

这项是最难满足的一项。

定义首先定义第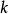 个动量 :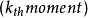

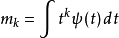
若 ，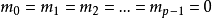

则我们说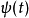 有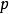 个消失动量。

如何计算消失动量我们可以看到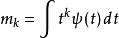 不太好计算，尤其是 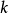很大的时候。

此时，可以善用傅立叶转换来进行计算。

计算第0个动量首先，观察傅立叶转换的公式:

当令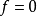 时，可以看到以上公式变成:

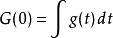
正是第0个动量 。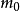

因此，若要计算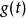 的第0个动量，可以先计算 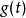的傅立叶转换，再取直流项(也就是 。

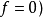计算第k个动量我们可以同样利用傅立叶转换来计算第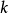 个动量。

首先，傅立叶转换有一个性质: 在频域微分 次，就相当于时域乘上 :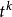

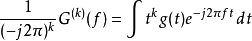
当令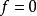 时，可以看到以上公式变成:

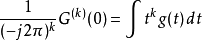
正是第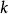 个动量 。

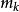因此，若要计算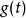 的第k个动量，可以先计算 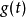的傅立叶转换的k次微分，再取直流项也就是 。

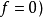一些常用函数的消失动量连续函数哈尔小波转换是最简单的一种小波转换，使用哈尔基底(Haar Basis)来做母小波。

而墨西哥帽函数(Mexican hat function)也常被用来当母小波。

哈尔基底

哈尔基底的数学表示式如下:

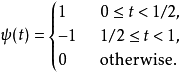
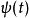是一个奇函数，所以

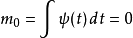
但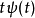 是偶函数，所以

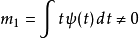
因此，哈尔基底的消失动量为1。

墨西哥帽函数

墨西哥帽函数的数学表示式:

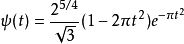
仔细观察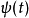， 其实是高斯函数的二次微分:

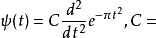常数。

而高斯函数做傅立叶转换仍是高斯函数:

。

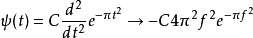利用

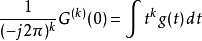
可以算出

。

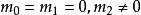所以墨西哥帽函数的消失动量为2。

高斯函数的p次微分

墨西哥帽函数是高斯函数的二次微分，所以消失动量为2。

当

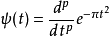
其傅立叶转换为

。

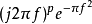利用

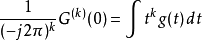
可以算出

。

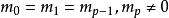所以高斯函数p次微分的消失动量为p。

连续函数的离散系数多贝西小波(Daubechies wavelet)、Symlet 都是一些常用的离散小波，而且都是由连续小波的离散系数推导而来。

多贝西小波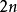 点的多贝西小波，消失动量 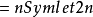点的Symlet，消失动量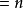

Symlet和多贝西小波非常类似，但是比多贝西小波还要对称。

消失动量对于函数的意义消失动量是用以判断一个函数如何递减的指标。举例来说，对于函数

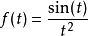
当输入值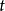 逐渐往无限大增加时，此函数会以 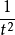的速率递减。 我们可用利用定义中的动量积分式 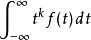来评估此函数的递减速率。

回到此范例中的函数，当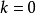 时，由于分子 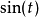会在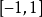 之间震荡，使得整个函数在 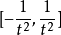震荡。

此性质使得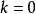 时，

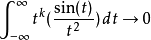
函数积分式必定会收敛于0，代表第0个动量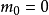

当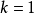 时，

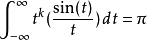
因此第1个动量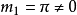

对于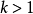 的情况，动量积分式均会随着 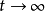而发散。

由以上的范例，我们可借由能够让动量积分式收敛为0的最大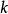 值来判断函数的递减速率，而此最大{\displaystyle k}值便是函数的消失动量。

在连续小波转换中，设计母小波的其中一个条件是有值区间比须是有限的，而母小波在有值区间内如何递减的特性，则可由消失动量来描述。

消失动量的等价叙述依照定义，小波母函数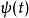 有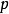 个消失动量的条件为

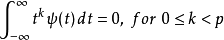
然而由于此定义中包含了一个无限范围的连续积分，因此在设计小波母函数上并不实用。

若定义小波转换中的尺度函数为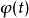 ，当以下小波母函数和尺度函数的关系成立时，

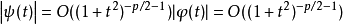
下列四项叙述便是等价的：

1. 小波母函数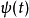 有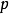 个消失动量。

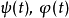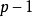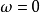2. 的傅立叶转换，以及前 次微分在 处均为零。

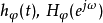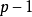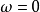3. 的傅立叶转换，以及前 次微分在 处均为零。

4. 对于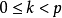 区间内的任意 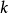值

是最高次方为{\displaystyle k}的多项式函数1。

本词条内容贡献者为:

黎明 - 副教授 - 西南大学