[科普中国]-傅汝兰尼积分

傅汝兰尼积分(Frullani integral)是一种特殊的含参变量的广义积分。傅汝兰尼积分公式是一种常见的积分公式，在计算广义积分时，有时可以化为Frullani积分，另外还有Euler积分、Dirichlet积分和Laplace积分等1。

基本介绍傅汝兰尼积分是一种特殊的含参变量的广义积分，形如

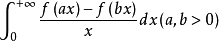的广义积分，其中f在(0，+∞)上连续。可精确计算的情形有2：

1.当f(0+)∈R， f(x)=f(+∞)∈R时，积分值为(f(0+)-f(+∞))ln(b/a)。

2.当f(0+)∈R，且存在A≥0，使

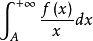收敛时，积分值为f(0+)ln(b/a)；

3.当f(+∞)∈R，且存在A>0，使

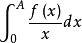收敛时，积分值为f(+∞)ln(b/a)2。

傅汝兰尼积分的证明定理1 设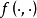 是定义在闭区间 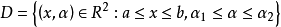的(二变数的)连续函数，让 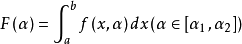，此时，下列性质成立3。

(i)F在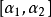 上连续。

(ii)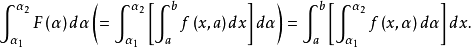

(iii)偏导函数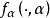 如在D连续，则F在[a，b]可微分而且

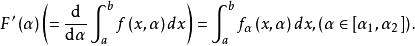
（以上定理的证明请参考相应文献）

Frullani的积分 f是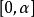 上的连续函数，若对任意的 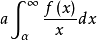存在，则

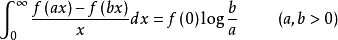称此为Frullani的积分3。

证明对任意α

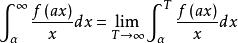
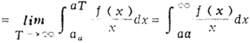
同理

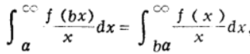
所以

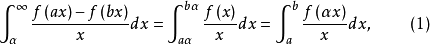
现令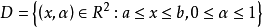 ，在D的各点(x，α)研究与它对应的实数值f(αx)/x的函数，这个函数在闭区间D是连续的。因此，根据以上定理的(i)，由3

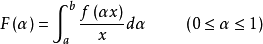所定义的函数F在[0，1)连续。故

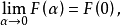即

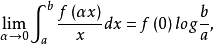这样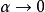， 时，(1)的左边收敛，且

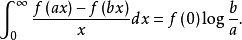
本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学