[科普中国]-麦克劳林级数

麦克劳林级数(Maclaurin series)是函数在x=0处的泰勒级数，它是牛顿(I.Newton)的学生麦克劳林(C.Maclaurin)于1742年给出的，用来证明局部极值的充分条件，他自己说明这是泰勒级数的特例，但后人却加了麦克劳林级数这个名称1。

基本介绍对于一个给定的函数f(x)，如果能找到一个幂级数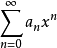 ，使

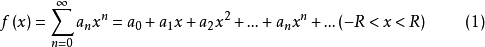成立，则称f(x)可展开成x的幂级数。但要将f(x)展开成x的一个幂级数，需解决两个以下问题：

(1)如何确定式(1)中的系数 ?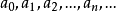

(2)按所求得的系数，这个幂级数在它的收敛域内的和函数是否就是f(x)?

先解决问题(1)，不妨设式(1)成立。那么。根据幂级数可以逐项求导的性质，依次求出式(1)中的各阶导数：

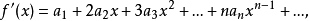
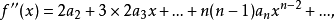
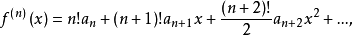把x=0代人式(1)及上述各式，得

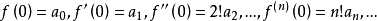于是

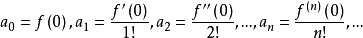把它们代回式(1)，得

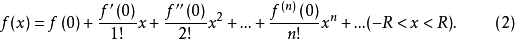
通常称式(2)为f(x)的麦克劳林展开式或f(x)在x=0处的幂级数展开式。式(2)中等号右端的级数称为f(x)的麦克劳林级数或f(x)展开成x的幂级数。

至于问题(2)。只要证明其余项满足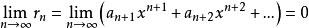即可(证明略)。

下面考虑在什么条件下，函数f(x)能展开成麦克劳林级数。

可见，按公式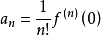求得系数的幂级数在它的收敛域内的和函数就是f(x)2。

麦克劳林级数展开的条件及方法定理1设函数f(x)的麦克劳林级数的收敛半径R>0，当n→∞时，如果函数f(x)在任一固定点x处的n阶导数f(n)(x)有界，则函数f(x)在收敛区间(-R，R)内能展开成麦克劳林级数3。即

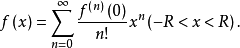
把函数f(x)展开成龙的幂级数，有直接展开法和间接展开法2。

直接展开法

利用麦克劳林级数公式将函数f(x)展开成x的幂级数的方法，称为直接展开法。步骤可归纳为：

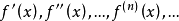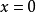(1)求出f(x)的各阶导数，令得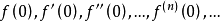

(2)写出f(x)的麦克劳林级数

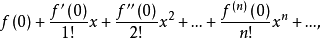并求出收敛半径R。

间接展开法

利用麦克劳林级数展开函数，需要求高阶导数，比较麻烦，如果能利用已知函数的展开式，根据幂级数在收敛域内的性质，将所给的函数展开成幂级数，这种方法称为间接展开法2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学