[科普中国]-重级数

重级数(multiple series)也称多重级数，k重级数等，是重序列的形式和，多重级数的理论和性质等可效仿二重级数的理论和性质加以推广得到。

基本介绍重级数（1）由m重序列an1n2…nm构成的形如

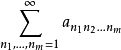的表达式称为m重级数，这里n1，n2，…，nm各自独立地取1，2，3，…，参见“二重级数”，该条中的各种部分和容易推广到m≥3时的m重级数1。

（2）设(xs)s∈ Np是G之元素的多重序列，对Np的任一有限子集J，假定

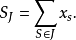称由多重序列(xs)及族(SJ)所组成的偶为以(xs)为通项的多重级数，其中J取遍Np的全体有限子集的集合。用通俗而不严格的语言，人们也常说如果族(xs)s∈Np是可和的，则这个多重级数是收敛的2。

相关性质定理设有r个下标的无穷数组

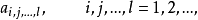则称运算符号

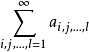为多重(r-重)级数(multiple series)，若部分和

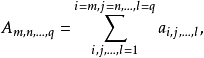当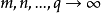时有有穷极限A，则称此多重级数收敛，且和为A，否则称为发散。

多重级数的理论可效仿下面的二重级数理论加以推广得到1。

二重级数是二重序列的形式和，设{amn}是二重序列，把它的项按任意次序排列并以加号连结得到的表达式称为二重级数，记为

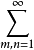amn， (1)

这里m，n各自独立地取正整数1，2，3，…数

Smn=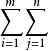aij

称为(1)的部分和，若二重极限

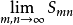=S(有限)，

则称该二重级数收敛，S为它的和，记为

S=.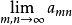

当这样的S不存在时，称这个二重级数发散。若

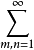|amn|

收敛，则称(1)绝对收敛。类似于通常的级数(相对于二重级数，通常的级数称为单级数)，可定义二重级数的条件收敛性。单级数的一些基本性质仍为二重级数所保持。例如，非负项二重级数收敛当且仅当其部分和有界，二重级数收敛的必要条件是amn→0(m，n→∞)，绝对收敛的二重级数必收敛(参见“绝对收敛级数”)等，对二重函数项级数，也可如函数项级数那样引进一致收敛概念，并得到相应的柯西准则、M判别法等，设φ是正整数集N+到N+×N+上的一一对应，则对二重级数(1)，可以得到级数

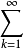aφ(k).

φ称为二重序列{amn}到序列{aφ(k)}k=1的重排，或二重级数(1)到单级数∑aφ(k)的重排.若级数

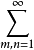|amn|，|amn|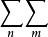，|amn|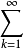，|aφ(k)|

之一收敛，则：

1.另三个也收敛，且它们的和相等(设为S)。

2.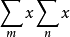amn与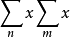amn均绝对收敛于S(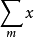amn与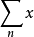amn也绝对收敛)。

在一些文献中，上述结论被称为主要重排定理。由此可知，绝对收敛的二重级数的两个叠级数也绝对收敛，有同一个和。由于二重级数的项的排列次序不惟一以及多种研究目的，因此，还有多种定义二重级数的部分和的方式，相应地也就有了不同的定义二重级数的和与收敛性的方式1。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学