[科普中国]-概括原则

概括原则(principle of comprehension)是古典集合论的基本原则，指古典集合论中用以构造集合的一个重要规定或公理，其内容为无条件承认任给一个性质P，人们就能把所有满足该性质P的对象，且仅由这些具有性质P的对象汇集在一起而构成一个集合.用符号来表示就是G={x|P(x)}，其中“|”左边的x表示集合G的任一元素，而“|”右边的P(x)表示元素x具有性质P，{ }表示把所有具有性质P的x汇集在一起而构成一集合。因此，概括原则的另一表达式为ᗄx(x∈A↔P(x))，亦即凡是集A之元素必具有性质P，反之，凡具有性质P的对象必为集A之元素。所以，概括原则是一条集合存在性公理(公理模式)。在德国数学家康托尔(Cantor，G.(F.P.))的早期工作中，概括原则只是隐蔽地被使用着，后来德国数学家、数理逻辑学家弗雷格(Frege，(F.L.)G.)公开地采用这一公理模式。对于概括原则内容的理解和使用，还应特别指出如下几点：1.概括原则中用以造集的那个性质P必须是精确性一元谓词，任何非精确性一元谓词都不是康托尔意义下用以造集的谓词，这个大前提无论是康托尔还是弗雷格都没有明文叙述，只是在使用概括原则时无形地贯彻。2.在概括原则之下用以造集的精确性一元谓词是完全任意的，而且对象域也是没有任何限制的。3.给定精确性一元谓词后，由概括原则所构造之集惟一确定，它恰由所有满足该谓词的对象组成1。

基本介绍概括原则是集合论的一项重要原则，是集合论创始人康托尔(G.F.P.Cantor)提出的确定集合的基本原则：对于任何性质P，都存在一个集合A，它恰好由具有性质P的所有元素组成，即A={x|P(x)}。康托尔提出的这一确定集合的原则失之过宽(例如，由它允许x是自己的元素这个性质出发，会导出一些悖论(如著名的罗素悖论)，而被认为是不正确的。分离公理弥补了概括原则的缺点(参见“分离公理”)，把集合限制为由已给集合与已给性质共同确定的对象。例如，它不允许一切集合的集合存在.用概括原则确定的对象称为类。任何性质P都确定一个类C={x|P(x)}。类可以是集合，可以不是集合，不是集合的类称为真类，例如，完全类V={x|x=x}就是真类，而空类∅={x|x≠x}就是集合：空集∅，对于类仍可如下定义包含关系与各种运算：

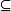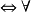1.ord Cord Dx(x∈ord C→x∈ord D)；

2.ord C∩ord D={x|x∈ord C∧x∈ord D}；

3.ord C∪ord D={x|x∈ord C∨x∈ord D}；

4.ord C-ord D={x|x∈ord C∧x∉ ord D}；

5.∪ord C={x|S(S∈ord C∧x∈S)}2。

相关分析为了给出一个集合，常常是列举出该集合的元素，这种方法的好处是具有明显性，比如，令集合S1：={0，1，4}，我们一眼就看出它只有三个元素，即0，1，4，但是，在有些情况下，这样做是很不方便的，比如令集合S2为：

{5832，6759，8000，9261，10648，12167，13824)，(1)

式(1)所确定的集合就有点烦琐了，这样大的数目再多列出几个，那就更复杂甚至无法写出3。

当我们分析一下S2的元素的性质时，就会发现这些数都是有规律的，它们是18到24之间的这七个自然数的立方数，亦即当x满足18≤x≤24时，S2的元素恰为x3，这样就有：

S2：={y|x是一自然数，且18≤x≤24并且y=x3}， (2)

其中竖杠的前边是集合S2的元素，它必须满足竖杠的后边所列举的条件，亦即“x是一自然数且18≤x≤24并且y=x3，这个条件也叫做一个性质。(2)表明S2的元素都具有性质为“把这个元素开立方，立方根为18与24(包括18和24在内)之间的自然数”.不难验证它的元素恰好是在(1)中所列举的那些．由外延原则，(1)与(2)定义了同样的集合。

当我们把(2)式中的条件改为“x是一自然数且10≤x≤109并且y=x3时，所定义的集合称为S'2，如果要用类似于(1)式那样的显式去列举S'2时，那将是很烦琐的事情了。如果把(2)式中的条件改为：“x是一有理数且10≤x≤1092000且y=x3”时，这时如果要使用(1)那样的显式，枚举这样的集合的全部元素就几乎不可能。为此，为了方便、简洁地给出一个集合，就需采用如像(2)这样的定义方式，上述所列举的条件都叫做性质，康托尔把所有满足给定性质的元素汇集在一起而成为一个集合，并且称之为概括原则。也就是说：

概括原则 任给一个性质P，那么存在着一个集合S，它的元素恰好是具有性质P的那样的一些对象，亦即

其P(x)是“x具有性质P”的一个缩写。这样，就有 。

这条原则在使用上是强有力的，而且也是很方便的。比如，集合{2，3，4，8}，可用条件“x=2或者x=3或者x=4或者x=8”来给出，可记成：

S2：={x|x=2或者x=3或者x=4或者x=8}．

在下边，我们用“∨”表示“或者”，用“∧”表示“并且”。

例如：{x|“x是一自然数”∧80≤x2≤200}就是集合{9，10，11，12，13，14)；

{x|x是一自然数}就是集合N；

{x|x=3}就是集合{3}。

应该指出，使用概括原则要有限制，否则会出毛病3。

罗素悖论与概括原则对于任意性质P(x)，都存在一个类(包括集合)C，使C={x|P(x)}，其中，P(x)是描述任意对象之属性的谓词，它表示x具有性质P。其形式化表示为

注释 对任意属性谓词P(x)，都可决定一个类，且满足：

x属于C 当且仅当 x满足P(x)

当用P(x)能够解释一个集合C时，也称P(x)为集合C的入集条件4。

19世纪后期，著名的英国数学家罗素(Russell)指出，看似严谨的概括原则所规定的未必是集合，其中存在悖论，并给出了解决的方法，这就是著名的罗素悖论。

设x是任意对象，是一个对x的属性描述。按照概括原则，可用P(x)去规定一个类T，，这时，由于T也是对象。故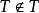与T∈T不能同时成立，也不能同时不成立。

如果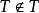成立，即T满足P(x)，这时，按照概括原则有T∈T，从而引出了矛盾。

如果T∈T成立，这时T是T的元素，那么按照概括原则T满足P(x)，即。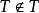

显然，由这个P(x)所规定的不是集合。

罗素的证明，拯救了数学基础理论所面临的一场灾难。弗雷格(Frege)在他的《算术的基本法则》第二卷即将付印之时，收到罗素先生的一封信，罗素将集合论的悖论告诉了他。弗雷格在他书的尾页上写道：“一个科学家不会碰到比这更难堪的事了。即在工作完成之际，它的基础垮了。”

罗素指出概括原则规定的是类，在这些类中有一些是真类，正如。它们不是集合。子集分离原则对概括原则作了补充，使集合悖论得以消除4。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学