若在实数集中,在某个区间上的函数都是有定义的,则这个区间就称为“定义区间”。
概念定义区间,顾名思义,在某个区间上的函数都是有定义的。孤立的点构不成区间。
初等数学“初等函数在其定义区间内可导”这句话是错的。y=|x|=√(x^2),这是一个初等函数,定义区间为(-∞,+∞),但在x=0处是不可导的。
高等数学高等数学中提到初等函数在定义区间(不是定义域)一定连续,函数如果在某些孤立的点有定义,那么这些点是在其定义域内的,但是这些孤立的点是不在其定义区间内的。总结就是:基本初等函数在其定义域内连续;初等函数在其定义区间内连续。
区别于国际标准组织另一种表达方式在法国及其他一些欧洲国家,和国际标准化组织编制的ISO 31-11,用{\displaystyle ][}代替{\displaystyle ()}来表示开区间,1例如:
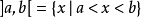
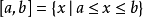
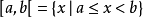
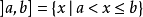 另外,在小数点以逗号来表示的情况下,为免产生混淆,分隔两数的逗号要用分号来代替,例如将
另外,在小数点以逗号来表示的情况下,为免产生混淆,分隔两数的逗号要用分号来代替,例如将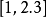 写成
写成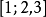 。若只把小数点写成逗号,就会变成
。若只把小数点写成逗号,就会变成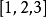 ,此时不易判断究竟是
,此时不易判断究竟是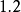 与
与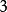 之间,还是
之间,还是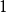 与
与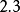 之间的闭区间。
之间的闭区间。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国