[科普中国]-牛顿一辛普森公式

牛顿-辛普森公式是一种适应面较广的求积公式。

这个公式不仅适用于作为拟柱体的棱柱、棱锥和棱台，而且适用于不是拟柱体的圆柱、圆锥、圆台和球台，甚至像椭球体等。

简介一个几何体被垂直于其高（或平行于其底）的平面所截，如果截面面积是它到上底（或下底）的距离的K次函数（K=0,1,2,3），即S(x)=ax3+bx2+cx+d，则它的体积为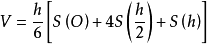 ，式中h为几何体的高，S(O)，S(h)是上、下底的面积，S(h/2)是中截面面积。1

证明只需要证明根据公式算出来的体积和用积分算出来的体积相等即可。

设截面面积是截面高h的不超过3次的函数：f(h)= ah3+bh2+ch+d，那么，利用积分计算体积，可以得到（积分限为0~h）：V=∫f(x)dx=ah4/4+bh3/3+ch2/2+dh；利用公式计算体积，可以得到：

V=H(S1+4S0+S2)/6=h(f(0)+4f(h/2)+f(h))/6=h[d+4(ah3/8+bh2/4+ch/2+d)+(ah3+bh2+ch+d)]/6

=ah4/4+bh3/3+ch2/2+dh。

因此两式相等，公式得证。

注：当函数f(h)次数高于或等于4次时，公式一般不成立。这只需验证f(h)=h4时公式不成立即可。

应用牛顿-辛普森公式是一种适应面较广的求积公式。

牛顿-辛普森公式不仅适用于作为拟柱体的棱柱、棱锥和棱台，而且适用于不是拟柱体的圆柱、圆锥、圆台和球台，甚至像椭球体等。

事实上，其他符合条件（所有顶点都在两个平行平面上、用平行于底面的平面去截该图形时所得到的截面面积是该平面与一底之间距离的不超过3次的函数）的立体图形也可以利用该公式求体积。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学