[科普中国]-沃尔斯滕霍尔姆定理

在数论上，Wolstenholme定理说明，对于大于或等于5的质数，有四个定理，具体内容请参见正文。这定理是19世纪英国数学家Joseph Wolstenholme提出的。值得一提的是Wolstenholme是吴尔芙的父亲的朋友，也是吴尔芙小说《灯塔行》中Augustus Carmichael的原形。

简介在数论上，Wolstenholme定理说明，对于大于或等于5的质数，有

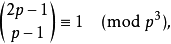
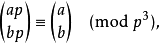
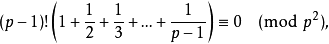
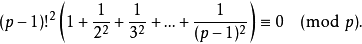以上四个等式是等价的。

只有少数质数符合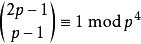，现时已知有两个这样的质数，16843 及 2124679 （OEIS:A088164）。这类质数称为Wolstenholme质数，下一个这样的质数如果存在，它大于10。

这定理是19世纪英国数学家Joseph Wolstenholme提出的。值得一提的是Wolstenholme是吴尔芙的父亲的朋友，也是吴尔芙小说《灯塔行》中Augustus Carmichael的原形。1

数论数论是纯粹数学的分支之一，主要研究整数的性质。被誉为“最纯”的数学领域。

正整数按乘法性质划分，可以分成质数，合数，1，质数产生了很多一般人也能理解而又悬而未解的问题，如哥德巴赫猜想，孪生质数猜想等，即。很多问题虽然形式上十分初等，事实上却要用到许多艰深的数学知识。这一领域的研究从某种意义上推动了数学的发展，催生了大量的新思想和新方法。数论除了研究整数及质数外，也研究一些由整数衍生的数（如有理数）或是一些广义的整数（如代数整数）。

整数可以是方程式的解（丢番图方程）。有些解析函数（像黎曼ζ函数）中包括了一些整数、质数的性质，透过这些函数也可以了解一些数论的问题。透过数论也可以建立实数和有理数之间的关系，并且用有理数来逼近实数（丢番图逼近）。

数论早期称为算术。到20世纪初，才开始使用数论的名称，而算术一词则表示“基本运算”，不过在20世纪的后半，有部分数学家仍会用“算术”一词来表示数论。1952年时数学家Harold Davenport仍用“高等算术”一词来表示数论，戈弗雷·哈罗德·哈代和爱德华·梅特兰·赖特在1938年写《数论介绍》简介时曾提到“我们曾考虑过将书名改为《算术介绍》，某方面而言是更合适的书名，但也容易让读者误会其中的内容”。

卡尔·弗里德里希·高斯曾说：“数学是科学的皇后，数论是数学的皇后。”1

质数质数（Prime number），又称素数，指在大于1的自然数中，除了1和该数自身外，无法被其他自然数整除的数（也可定义为只有1与该数本身两个正因数的数）。大于1的自然数若不是素数，则称之为合数。例如，5是个素数，因为其正约数只有1与5。而6则是个合数，因为除了1与6外，2与3也是其正约数。算术基本定理确立了素数于数论里的核心地位：任何大于1的整数均可被表示成一串唯一素数之乘积。为了确保该定理的唯一性，1被定义为不是素数，因为在因式分解中可以有任意多个1（如3、1×3、1×1×3等都是3的有效约数分解）。

古希腊数学家欧几里得于公元前300年前后证明有无限多个素数存在（欧几里得定理）。现时人们已发现多种验证素数的方法。其中试除法比较简单，但需时较长：设被测试的自然数为n，使用此方法者需逐一测试2与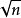之间的整数，确保它们无一能整除n。对于较大或一些具特别形式（如梅森数）的自然数，人们通常使用较有效率的算法测试其是否为素数（例如2-1是直至2017年底为止已知最大的梅森素数）。虽然人们仍未发现可以完全区别素数与合数的公式，但已建构了素数的分布模式（亦即素数在大数时的统计模式）。19世纪晚期得到证明的素数定理指出：一个任意自然数n为素数的概率反比于其数位（或n的对数）。

许多有关素数的问题依然未解，如哥德巴赫猜想（每个大于2的偶数可表示成两个素数之和）及孪生素数猜想（存在无穷多对相差2的素数）。这些问题促进了数论各个分支的发展，主要在于数字的解析或代数方面。素数被用于资讯科技里的几个程序中，如公钥加密利用了难以将大数分解成其素因数之类的性质。素数亦在其他数学领域里形成了各种广义化的素数概念，主要出现在代数里，如素元及素理想。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学