[科普中国]-正则素数

在数论中，正则素数的概念首先由恩斯特·库默尔在1847年为了处理费马最后定理而引入。它具有许多种等价的定义方式。

简介在数论中，正则素数的概念首先由恩斯特·库默尔在1847年为了处理费马最后定理而引入。它具有许多种等价的定义方式。其中之一是：

**定义：**素数p是正则素数，当且仅当p不整除分圆域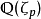的类数。

此定义美则美矣，却不容易计算。另一种定义方式是：素数p是正则素数，当且仅当p不整除伯努利数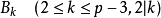的分子。

头几个正则素数为：

3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, ... （OEIS中的数列A007703）

库默尔证明了：当p是正则素数时，不存在非零整数解。最小的10个非正则素数是37、59、67、101、103、131、149、157、233、257（OEIS中的数列A000928）。 已知存在无穷多个非正则素数，而迄今仍未知是否存在无穷多个正则素数。1

费马大定理费马大定理，也称费马最后定理（法语：Le dernier théorème de Fermat)；(英语：Fermat's Last Theorem），其概要为：

当正整数n>2时，关于x，y，z的不定方程

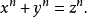没有正整数解

以上陈述由17世纪法国数学家费马提出，一直被称为“费马猜想”，直到英国数学家安德鲁·怀尔斯（Andrew John Wiles）及其学生理查·泰勒（Richard Taylor）于1995年将他们的证明出版后，才称为“费马大定理”。这个猜想最初出现费马的《页边笔记》中。尽管费马表明他已找到一个精妙的证明而页边没有足够的空位写下，但仍然经过数学家们三个多世纪的努力，猜想才变成了定理。在冲击这个数论世纪难题的过程中，无论是不完全的还是最后完整的证明，都给数学界带来很大的影响；很多的数学结果、甚至数学分支在这个过程中诞生了，包括代数几何中的椭圆曲线和模形式，以及伽罗瓦理论和赫克代数等。这也令人怀疑当初费马是否真的找到了正确证明。而安德鲁·怀尔斯由于成功证明此定理，获得了包括邵逸夫奖在内的数十个奖项。1

恩斯特·库默尔恩斯特·爱德华·库默尔（Ernst Eduard Kummer，1810年1月29日－1893年5月14日），德国数学家。库默尔的研究领域主要有三个方面：函数论、数论和几何。在函数论方面，他研究了超几何级数，首次计算了该级数单值群的代入值。在几何方面，他研究了一般射线系统，并用纯代数方法构作了一个四次曲面，它有16个孤立的二重点，16个奇异切平面，现在称之为库默尔曲面。库默尔在数论上花的时间最多，贡献也最大。最重要的是他提出了理想数的概念。当时库默尔所关心的问题首先是高斯研究过的高次互反律，其次是费马大定理。1

数论数论是纯粹数学的分支之一，主要研究整数的性质。被誉为“最纯”的数学领域。正整数按乘法性质划分，可以分成质数，合数，1，质数产生了很多一般人也能理解而又悬而未解的问题，如哥德巴赫猜想，孪生质数猜想等，即。很多问题虽然形式上十分初等，事实上却要用到许多艰深的数学知识。这一领域的研究从某种意义上推动了数学的发展，催生了大量的新思想和新方法。数论除了研究整数及质数外，也研究一些由整数衍生的数（如有理数）或是一些广义的整数（如代数整数）。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学