[科普中国]-低基定理

低基定理是关于不可解度的定理，不可解度，或图灵度，是数学逻辑的名词，尤其应用在可计算性理论中，低基定理的具体定义请参见正文。

简介低基定理是关于不可解度的定理，不可解度，或图灵度，是数学逻辑的名词，尤其应用在可计算性理论中。1

定理设为无穷长二进制串的集合，若自然数的语言中存在递归公式θ，使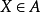当且仅当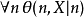为真，则定义A为类。

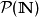若将无穷长二进制串的第n位理解成“n是否属于该集合”，则自然对应了自然数集合的子集集合。因此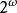上可以引入不可解度的关系。

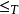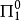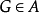低基定理表明，若A是一个类，则存在使得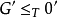。称G为A的低基。1

不可解度不可解度，或图灵度，是数学逻辑的名词，尤其应用在可计算性理论中。1

可计算性理论在计算机科学中，可计算性理论（Computability theory）作为计算理论的一个分支，研究在不同的计算模型下哪些算法问题能够被解决。相对应的，计算理论的另一块主要内容，计算复杂性理论考虑一个问题怎样才能被有效的解决。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学