[科普中国]-直线划分平面

直线划分平面是解析几何研究的重要问题之一。任一直线l：Ax+By+C=0把平面内的点分成三个点的集合：(1)直线上的点的集合，点到直线的距离δ=0；(2)不包含原点在内的那个半平面的点的集合，δ>0；(3)包含原点在内的那个半平面的点的集合，δ0；另一个半平面内的点的坐标满足不等式Ax+By+C0时，直线l与线段P1P2相交，即点P1，P2在直线l的异侧；当Ax1+By1+C与Ax2+By2+C同号，即λ0，另一个半平面内的点的坐标适合不等式Ax+By+C0，则点P在直线l的右侧(x轴正向所指的一侧)的充分必要条件是Ax0+By0+C>0；

2.若B>0，则点P在直线l的上侧(y轴正向所指的一侧)的充分必要条件是Ax0+By0+C>0；

3.若C>0，则点P与原点在直线l的同侧的充分必要条件是Ax0+By0+C>0；

4.直线l的法向量(A，B)所指的一侧的点的坐标满足Ax+By+C>0，另一侧的点的坐标满足Ax+By+C0在有向直线的左侧1。

相关性质及其证明我们已经知道，如果点不在直线l:Ax+ By+C=0上，那么Ax0+ By0+C≠0.现在进一步证明以下重要结论:

把在直线l不同侧的任意两点的坐标代入二元一次式Ax + By+C，得到的数值异号；把在直线l同侧的任意两点的坐标代入二元一次式Ax+By+C，得到的数值同号2。

证明设已知两点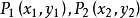及直线l:Ax+ By+C=0。

(1)如果经过P₁、P₂的直线与直线l相交，设交点为P,点P分所成的比为λ，则点P的坐标为

因为点P在直线l上，所以点P的坐标必满足直线l的方程，即有

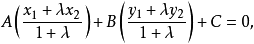整理后,得，所以

由此可见:当点P₁、P₂分别在直线l的两侧时，点P内分，分比λ>0，因此与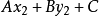异号；当点P、Pr在直线l的同侧时，点P外分，分比λ0，另一个半平面内的点的坐标满足Ax+ By+C0，说明原点所在一侧的区域Ax+ By+C>0,另一侧Ax+By+C