[科普中国]-球面图形

球面图形(spherical figure)是球面几何的研究对象，指所有点都在同一球面上的几何图形，在球面几何学中，主要研究的球面图形有球面大圆、小圆、球面多边形、球面二角形和球面三角形等1。

基本介绍与空间一点O有等距离R的点的全体，叫做球面。所有点都在同一球面上的图形，叫做球面图形。

点O叫做球心，距离R叫做球的半径，两端点在球面上的线段，叫做球的弦。过球心的弦，叫做球的直径，直径的两端点，叫做对径点。

球面图形的基本元素用一平面去截球面，如果平面经过球心，那么，球面与平面的公共部分叫做大圆。如果平面不经过球心又与球面相交，那么，球面与平面的公共部分叫做小圆。

大圆与球面上的点是球面图形的基本元素，它与平面图形的点和直线相当，点与大圆有如下的关系。

1)通过任意给定的不是对径的球面两点有一大圆。

2)通过任意给定的不是对径的球面两点至多有一大圆。

3)若C₁与C₂是球面上任意两个大圆，至少有一点是它们的交点。

4)每一大圆至少包含三个点。

5)若C是任一大圆，球面上至少有一点不属于大圆C。

6)在球面上至少有一个大圆。

以上六个关系，如果不借助球面外的任一点(如球心)可以把它们作为公理看待，如果借助于球面外的任一点 (如球心)，则以上关系可以证明，例如关系(3)，过球心O的任意两平面有公共点O，因而有公共直径的两端点，于是任意两个大圆都通过它们公共直径的对径点。即是说在球面上没有不相交的两个大圆，现在利用球心来研究球面图形2。

其他球面图形及性质定义2过球心的两射线与球面相交于两点A、B，两点A、B与∠AOB内部的大圆部分叫做大圆的劣弧。除劣弧外的大圆部分叫做这大圆的优弧。显然劣弧小于半大圆2。

定义3用大圆劣弧连接不在同一大圆上的球面三点A,B，C得一球面图形，叫做球面三角形。如图1三点A、B、C叫做球面三角形的顶点，劣弧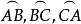 叫做球面三角形的边，有公共顶点的两边组成的角，叫做球面三角形的角，它的大小等于过顶点而切于两弧的切线夹角。

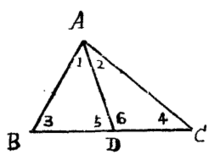
与球面三角形相对应的有一个三面角。

如图2，从球心O经球面三角形的三顶点A、B、C引射线，得到一个以球心为顶点的三面角O-ABC，这个三面角叫做球心三面角，三面角的三个面角对应于球面三角形的三边，三面角的三个二面角对应于球面三角形的三内角。

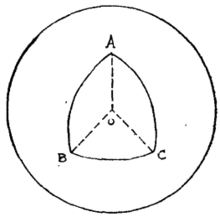
定义4 垂直于大圆所在平面的直径的两个端点，叫做这个大圆的极.

从定义4看出，大圆上任一点与它的极之间的大圆部分是这个大圆的1/4。

设有球面三角形ABC，如图3；边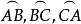的极分别为C'，A'，B'，且点A’，A在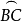的同侧，点B'、B在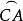的同侧， 点C'、C在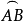的同侧， 则球面三角形A'B'C'叫做球面三角形ABC的极三角形。

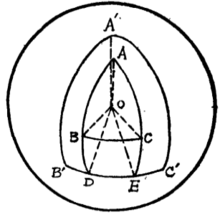
定理1 若球面三角形A'B'C' 是球面三角形ABC的极三角形，则球面三角形ABC也是球面三角形A'B'C'的极三角形。

证明: 如图3。

(1)因为A'是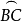 的极且与A在 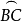的同侧，所以 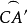是大圆弧的，且 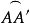为劣弧。

(2)点B'是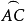 的极且与B在 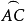的同侧，所以 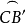是大圆弧的1/4，且 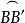为劣弧。

由(1)、(2)知点C是 的极，且与C'在 的同侧，同理点A是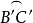 的极，且与A'在 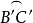的同侧。点B是 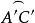的极，且与B'在 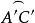的同侧，故球面三角形ABC是球面三角形A'B'C'的极三角形。

(证毕)2。

定理2 球面三角形的角与它的极三角形的对应边，就度量来说，它们互补。

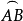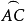**证明:**如图3,延长与使分别交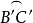于D、E，则球面角∠A与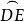的弧度数相同，要证明球面角∠A与边 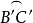互补，只须证

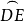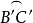+=1/2大圆=2直角

1)∵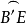=大圆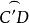，=1/4大圆

2)∴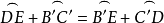=1/2大圆= 2直角

3)同理，球面角∠B与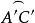互补

球面角∠C与互补

(证毕)。

定理3 球面三角形三个内角的和，大于2直角而小于6直角。

证明: 设有球面三角形ABC，要证明∠A,∠B，∠C的和在2直角和6直角之间。

作球面三角形ABC的极三角形A'B'C'，则从定理2得:

1)∠A+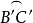= 2直角

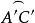∠B+= 2直角

∠C+= 2直角

2)以上三式两边分别相加得

∠A+∠B+∠C=6直角-()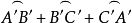

3)由于0