[科普中国]-可加季节模型

由时间序列趋势、季节因素和不规则因素组成的模型时间序列加法模型。不规则因素通常为不相关的，并且是独立同分布的称为可加季节模型。

理论如果我们不仅仅满足予分解现有的时间序列，而且想要对未来进行预测，就需要建立模型。首先。这里介绍比较简单的指数平滑(exponential smoothing)。指数平滑只能用于纯粹时间序列的情况，而不能用于含有独立变量时间序列的考察变量之间关系的研究。指数平滑的原理为：当利用过去观测值的加权平均来预测未来的观测值时(这个过程称为平滑)，离得越近的观测值要给以更多的权。而“指数”意味着：按照已有观测值“陈旧”程度增加的方向，在其上所加的权数按指数速度递减。以简单的没有趋势和没有季节成分的纯粹时间序列为例，指数平滑在数学上实际是一个几何级数。这时，如果用K表示在I时间的平滑后的数据(或预测值)，那么指数平滑模型为

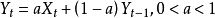
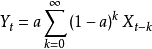
上面的公式是最简单的指数平滑形式，无法应对具有各种成分的复杂情况。针对各种成分的情况有各种实用的指数平滑模型公式。

公式我们根据数据，可以得到这些模型参数的估计以及对未来的预测。下面给出各种实用的指数平滑模型的公式。

对于时间序列Xt，趋势、光滑后的序列、季节因子分别用Tt、St、It表示；另外，p表示周期，et为残差。1

几种指数平滑模型如下：

(1)线性趋势可加季节模型(1inear trend，additive seasonality model)为

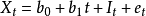
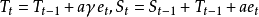
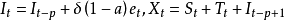
(2)指数趋势可加季节模(exponential trend，additive seasonality model)为

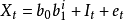
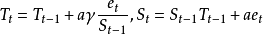
相关概念指数平滑：指数平滑法是在加权移动平均法基础上改进而来的一种广泛使用的统计分析方法。它通过计算一系列指数平滑值来消除不规则变动，以反映时间序列的长期趋势。指数平滑法既是对时间序列进行修匀的一种方法，也可以直接用于预测，还可以用于估计预测模型的参数。2

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学