[科普中国]-因子图

将一个具有多变量的全局函数因子分解，得到几个局部函数的乘积，以此为基础得到的一个双向图叫做因子图。在概率论及其应用中, 因子图是一个在贝叶斯推理中得到广泛应用的模型。

简介将一个具有多变量的全局函数因子分解，得到几个局部函数的乘积，以此为基础得到的一个双向图叫做因子图。在概率论及其应用中,因子图是一个在贝叶斯推理中得到广泛应用的模型。1

定义因子图使用一种二模图用来表示函数因式分解后的结果。 设有函数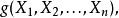

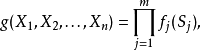其中其对应的因子图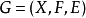包括变量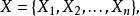节点因子节点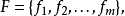和边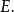边通过下列因式分解结果得到：在因子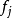节点和变量节点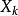之间存在边的充要条件是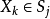存在。1

贝叶斯网络贝叶斯网络（Bayesian network），又称信念网络（belief network）或是有向无环图模型（directed acyclic graphical model），是一种概率图型模型，借由有向无环图（directed acyclic graphs, or DAGs）中得知一组随机变量及其n组条件概率分布（conditional probability distributions, or CPDs）的性质。举例而言，贝叶斯网络可用来表示疾病和其相关症状间的概率关系；倘若已知某种症状下，贝叶斯网络就可用来计算各种可能罹患疾病之发生概率。1

参考信念传播

贝叶斯推理

条件概率

马尔科夫链

贝叶斯网络

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学