[科普中国]-三角形行列式

三角形行列式(triangular determinant)是一种特殊的行列式，包括上三角形行列式和下三角形行列式，亦称上三角行列式和下三角行列式，统称三角形行列式。每个行列式都可以只运用行或者列的性质化为一个与其相等的上(下)三角形行列式，上(或下)三角形行列式都等于它们主对角线上元素的乘积1。

基本介绍下三角形行列式主对角线上方元素全为零的行列式，也即非零元素只出现在主对角线及下方的行列式，称为下三角形行列式(当ij时， )。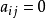

对上三角形行列式也总有：

证明：行列式及其余子式均依次按第一行展开即得(或因为上三角形行列式与下三角形行列式互为转置行列式)2。

对角形行列式主对角形行列式：主对角线上方、下方的元素全为零的行列式称为主对角形行列式。

主对角形行列式既是上三角形行列式又是下三角形行列式。

副对角形行列式：副对角线上方、下方的元素全为零的行列式称为副对角形行列式。

化为上(下)三角形行列式在计算行列式(特别是数字行列式)时，可先利用行列式的性质，把行列式化为上(下)三角形行列式，再利用上面的结果进行计算3。

解题思路：利用行列式的性质，可逐步将所给行列式化为三角形行列式，化零时一般尽量选含有1的行(列)及含零较多的行(列)，若没有1，则可适当选取便于化为零的数，或利用行列式的性质将某行(列)中的某数化为1；若所给行列式中元素间具有某些特征，则应充分利用这些特征，常见的有：

(1)行列式所有行(或列)全部元素化为1；

(2)对爪形(三线型)行列式，可通过将其余各行(或列)的某一倍数加到第1行(或列)而化为三角形行列式；

(3)若行列式的各行(或列)之间差别不大，可采用逐行(或列)相加(或减)的方法，将其化简后进行计算；

(4)对某些行列式，可在原行列式中增加一行一列，且保持原行列式不变，使其具有某种特征，便于计算，一般称此法为加边法；

总之，掌握行列式的特征是计算行列式的关键，在此基础上，充分利用行列式的性质，灵活选用方法，值得注意的是，同一个行列式有时会有不同的求解方法，可选取相对简单的方法或自己最熟悉的方法3。

【例1】计算行列式：

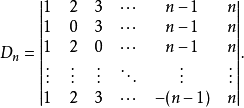
解：将第一行分别加到第2,3,4,...,n行，有

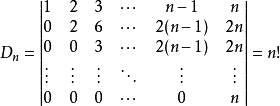
【例2】计算行列式：

解：将第2行乘-1加到第1行，再第4行乘-1加到第3行，分别有

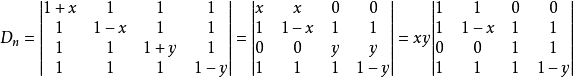
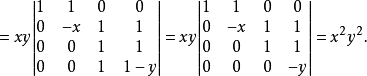
本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学