海涅-康托尔定理,以爱德华·海涅和乔治·康托尔命名,说明如果M是一个紧度量空间,则每一个连续函数都是一致连续的。1
定义M是一个紧度量空间,则每一个连续函数
f:M→N
其中N是度量空间,都是一致连续的。
例如,如果f : [a,b] → R是一个连续函数,则它是一致连续的。1
证明假设f在紧度量空间M上连续,但不一致连续,则以下命题
 ,使得对于所有M内的x和y,都有
,使得对于所有M内的x和y,都有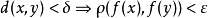
的否定是:
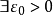 ,使得
,使得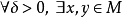 ,使得
,使得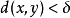 且
且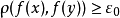 。
。
其中d和 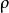 分别是度量空间M和N上的距离函数。
分别是度量空间M和N上的距离函数。
选择两个序列xn和yn,使得:
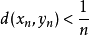 且
且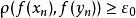
由于度量空间是紧致的,根据波尔查诺-魏尔施特拉斯定理,存在两个收敛的子序列(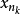 收敛于x0,
收敛于x0,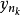 收敛于y0),因此:
收敛于y0),因此:
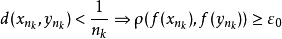 但由于f是连续的,且
但由于f是连续的,且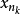 和
和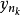 收敛于相同的点,因此这是不可能的。2
收敛于相同的点,因此这是不可能的。2
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国