[科普中国]-霍普夫－里诺定理

数学中，霍普夫—里诺(Hopf–Rinow)定理是关于黎曼流形的测地完备性的一套等价命题1，以海因茨·霍普夫和他的学生维利·里诺命名。

简介霍普夫－里诺定理如下：

设M是黎曼流形，则下列命题等价：

1.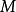 的有界闭子集是紧的。

2.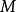 是完备度量空间。

3.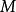 是测地完备：对 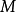中任意点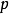 ，指数映射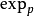 可定义在整个切空间 。

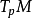而且，以上任一条均可导出对于中任何两点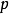 和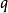 ，存在连起两点的测地线使长度最短（测地线一般是极值，不一定是最小值）。

推广霍普夫—里诺定理推广至长度度量空间如下：

若一长度度量空间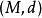 是完备和局部紧，那么 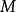中任意两点可以用长度最短的测地线连起，的任意有界闭子集是紧的。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学