[科普中国]-杜哈梅积分

在振动理论中，杜哈梅积分（Duhamel's integral）是求解线性系统在任意外载激励下响应的一种方法。

概要介绍问题背景受随时间变化的外载p(t)和粘性阻尼作用下的线性单自由度（SDF1）系统的运动方程是一个二阶常微分方程，可写为

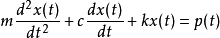
其中m为等效振子的质量，x代表系统振幅，t代表时间，c是粘性阻尼系数，k是系统刚度。

若初始静止于平衡位置的系统在t=0时刻受到一个单位冲击载荷作用，即p(t)是一个狄拉克δ函数δ(t)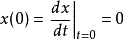，，可以解得系统响应（称为单位脉冲响应函数）为

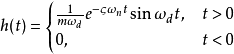
其中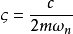称为系统的阻尼比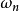，是系统在无阻尼状态下振动的固有圆频率，是系统在当前存在的阻尼c作用下的实际振动圆频率。推广到任意时刻τ时受到冲击载荷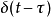作用的脉冲响应为

，

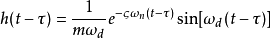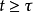
结论导出将任意载荷p(t)视为一系列脉冲激励的迭加2：

那么根据线性性质可知，系统的响应同样可以表示成对这一系列脉冲激励的响应函数的迭加：

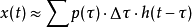
在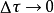时，连续求和转化为积分，此时上面的等式是严格成立的

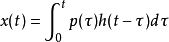
将h(t-τ)的表达式代入即得杜哈梅积分的一般形式：

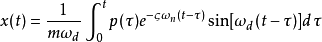
本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学