[科普中国]-高斯-卢卡斯定理

高斯-卢卡斯定理，又称卢卡斯定理，该定理描述了复系数多项式的一个性质：多项式导数的根一定在原多项式的根所构成的凸包内。

这一结论曾在1836被Carl Friedrich Gauss直接使用，1874 得到证明。

动机我们注意到，二次多项式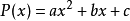 的导数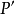的根为原多项式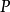的两个根的平均数。

同样地，如果一个次多项式有个两两不同的实值零点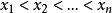，根据罗尔定理，其导数的每个零点都位于区间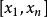之中。

高斯-卢卡斯定理可以看成这一性质在复系数多项式上的推广。

表述设 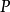是一个非常数的复系数多项式，那么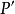所有的根属于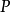的根构成的凸包。

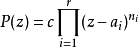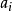证明将多项式函数P写成复数下的不可约形式： ，其中复数是多项式的主系数、是多项式的根、 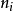为各个根的重数1。

首先注意到：

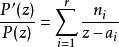
假设复数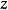满足：

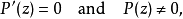
因此：

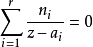乘以共轭取模：

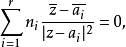
写成如下形式：

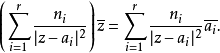
此时，我们可以将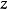看成是个位于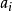的质点的重心，因此在其构成的凸包内。

另一种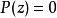情况下的证明是显然的。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学