[科普中国]-惟一分解定理

惟一分解定理有多种指代意义，一个是指整数惟一分解定理，即算术基本定理，也可以指多项式的惟一分解定理，是多项式理论的主要命题之一，还可以指交的惟一分解定理，它是交换诺特环理论的基本定理，也是理想论的核心，也指乘积的惟一分解定理，它是交的惟一分解定理在有单位元的诺特环中的应用。

整数惟一分解定理整数惟一分解定理亦称算术基本定理，是数论的重要定理之一。该定理断言：任何一个大于1的整数n都可以分解成若干个素因数的连乘积，如果不计各个素因数的顺序，那么这种分解是惟一的，即若n>1，则有

n=p1p2…pm， (1)

其中p1≤p2≤…≤pm皆素数，上式常简记为

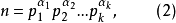其中，p1