[科普中国]-分离重因式法

分离重因式法(method of separating multiple factor)是多项式因式分解的一种方法1，判断一个多项式有无重因式可以通过辗转相除法。

基本介绍设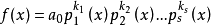 是f(x)的标准分解式，且其中不可约因式的最高重数m>1。令Fi(x)为f(x)的一切i重因式之积(i=1，2，…，m)，若f(x)中没有j重因式，就令Fj(x)=1。于是由f(x)的标准分解式得 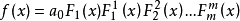。按以下的方法，可以具体地求出F1(x)，F2(x)，…，Fm(x)，令

d1(x)=(f，f′)=F2(x)F²₃(x)…Fm-1m(x)，

d2(x)=(d1，d1′)=F3(x)F²4(x)…Fm-2m(x)，

………………………………………

dm-1(x)=(dm-2，dm-2′)=Fm(x)，

dm(x)=1，

则

φ1(x)=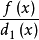 =a0F1(x)F2(x)…Fm(x)，

φ2(x)=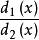 =F2(x)F3(x)…Fm(x)，

………………………………………

φm-1(x)=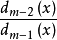 =Fm-1(x)Fm(x)，

φm(x)=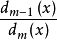 =Fm(x).

于是

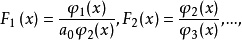
这种按以上方法和步骤求出Fi(x)的方法，称为分离重因式法，亦称重因式的分离1。

相关定理定理1 若不可约多项式p(x)是f(x)的k重因式（k≥1），则它是f'(x)的k-1重因式。特别地，f(x)的单因式不是f'(x)的因式。

此定理的逆命题不成立。

定理 次数大于0的多项式f(x)没有重因式的充分必要条件是f(x)与f'(x)互素2。

证明 设f(x)是一个n(n>0)次多项式，其典型分解式为：

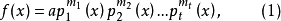由定理1有

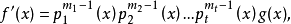此处g(x)不能被任何pi(x)（i=1，2，…，t）整除，由求最大公因式的方法，得

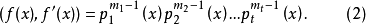因此，若f(x)没有重因式，亦即 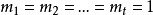，从而f(x)与f'(x)互素，反之，若f(x)与f'(x)互素，必有 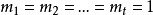，则f(x)没有重因式．

此定理给出了判断一个多项式有无重因式的实际方法，即通过辗转相除法便可解决。

由于多项式的导数以及两个多项式的最大公因式不因数域的扩大而改变，所以一个多项式有无重因式，也不会因数域的扩大而改变。

如果f(x)有重因式，则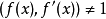 ，由(1)与(2)可以看出，用 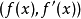去除f(x)所得商式为

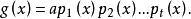
g(x)是一个没有重因式的多项式，且它与f(x)有完全相同的不可约因式。这种去掉因式重数的方法称为分离重因式法，由于g(x)的次数低于f(x)的次数，所以g(x)的不可约

因式可能比较容易求出，如果已经知道g(x)的一个不可约因式，那么决定它在f(x)中的重数并不难，只要应用带余除法就可以计算出来，此方法既然可以求出重因式，故在某些情况下，可以用来分解因式2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学