数学中,Θ函数是一种多复变特殊函数。其应用包括阿贝尔簇与模空间、二次形式、孤立子理论;其格拉斯曼代数推广亦出现于量子场论,尤其于超弦与D-膜理论。Θ函数最常见于椭圆函数理论。相对于其“z” 变量,Θ函数是拟周期函数(quasiperiodic function),具有“拟周期性”。在一般下降理论(descent theory)中,此来自线丛条件。1
雅可比Θ函数雅可比Θ函数取二变量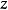 与
与 ,其中
,其中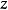 为任何复数,而
为任何复数,而 为上半复平面上一点;此函数之定义为:
为上半复平面上一点;此函数之定义为:
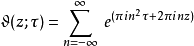 若固定
若固定 ,则此成为一周期为1的单变量
,则此成为一周期为1的单变量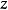 整函数的傅里叶级数:
整函数的傅里叶级数:
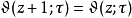 在以
在以 位移时,此函数符合:
位移时,此函数符合:
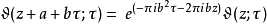 其中a与b为整数。2
其中a与b为整数。2
辅助函数可定义辅助函数:
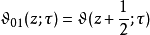
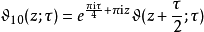
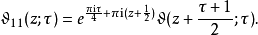 其中符号依黎曼与芒福德之习惯;雅可比的原文用变量
其中符号依黎曼与芒福德之习惯;雅可比的原文用变量 替换了
替换了 ,而称本条目中的Θ为
,而称本条目中的Θ为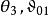 为
为 为
为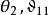 为
为 。
。
若设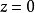 ,则我们可从以上获得四支单以
,则我们可从以上获得四支单以 ,为变量之函数,其中
,为变量之函数,其中 ,取值于上半复平面。此等函数人称“Θ‘常量’”(theta constant);我们可以用Θ函数定义一系列模形式,或参数化某些曲线。由“雅可比 恒等式”可得:
,取值于上半复平面。此等函数人称“Θ‘常量’”(theta constant);我们可以用Θ函数定义一系列模形式,或参数化某些曲线。由“雅可比 恒等式”可得:
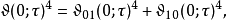
是为四次费马曲线。3
雅可比恒等式雅可比恒等式描述模群在Θ函数之作用;模群之生成元为T: τ ↦ τ+1与S: τ ↦ -1/τ。我们已有 T 作用之式。设:

则
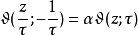
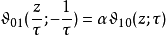
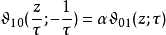
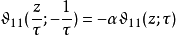
以nome q表示Θ函数我们可用变量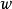 与
与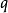 ,代替
,代替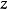 与
与 ,来表示ϑ。设
,来表示ϑ。设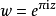 而
而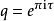 。则ϑ可表示为:
。则ϑ可表示为:
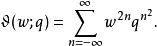 而辅助Θ函数可表示为:
而辅助Θ函数可表示为:
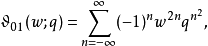
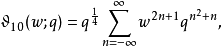
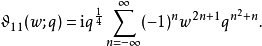
此表示式不需要指数函数,所以适用于指数函数无每一处定义域,如p进数域。4
乘积表示式雅可比三重积恒等式(Jacobi's triple product identity)中指出:若有复数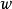 与
与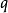 ,其中
,其中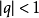 而
而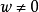 ,则
,则
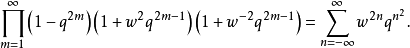
此式可以用基本方法证明,如戈弗雷·哈罗德·哈代和爱德华·梅特兰·赖特共同编著的《数论导引》。
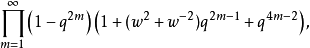
若用nome变量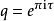 与
与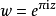 表示,则有:
表示,则有:
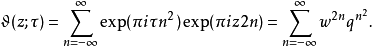
由此得到Θ函数的积公式:
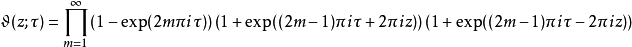
三重积等式左边可以扩展成:
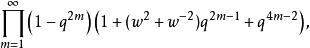 即:
即:
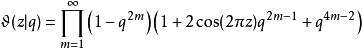 这个式子在z取实值时尤为重要。 各辅助Θ函数亦有类似之积公式:
这个式子在z取实值时尤为重要。 各辅助Θ函数亦有类似之积公式:
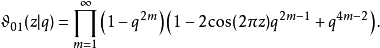
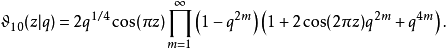
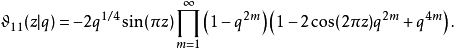
积分表示式雅可比Θ函数可用积分表示,如下:
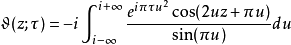
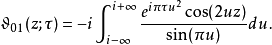
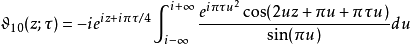
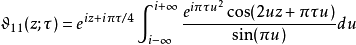
与黎曼ζ函数的关系黎曼尝用关系式
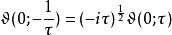 以证黎曼ζ函数之函数方程。他写下等式:
以证黎曼ζ函数之函数方程。他写下等式:
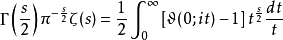 而此积分于替换
而此积分于替换 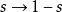 下不变。z非零时之积分,在赫尔维茨ζ函数一文有描述。
下不变。z非零时之积分,在赫尔维茨ζ函数一文有描述。
与维尔斯特拉斯椭圆函数之关系雅可比用Θ函数来构造椭圆函数,并使其有易于计算之形式。他表示他的椭圆函数成两枚上述Θ函数之商。魏尔施特拉斯椭圆函数亦可由雅可比Θ构造:
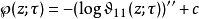 其中二次微分相对于z,而常数c使
其中二次微分相对于z,而常数c使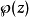 的罗朗级数(于 z = 0)常项为零。
的罗朗级数(于 z = 0)常项为零。
与模形式之关系设η为戴德金η函数。则
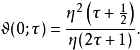
解热方程雅可比Θ函数为一维热方程、于时间为零时符合周期边界条件之唯一解。 设z = x取实值,τ = it而t取正值。则有
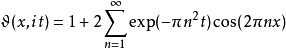 此解此下方程:
此解此下方程:
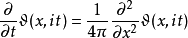 于t = 0时,Θ函数成为“狄拉克梳状函数”(Dirac comb)
于t = 0时,Θ函数成为“狄拉克梳状函数”(Dirac comb)
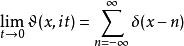 其中δ为狄拉克δ函数,故可知此解是唯一的。 因此,一般解可得自t = 0时的(周期)边界条件与Θ函数的卷积。5
其中δ为狄拉克δ函数,故可知此解是唯一的。 因此,一般解可得自t = 0时的(周期)边界条件与Θ函数的卷积。5
与海森堡群之关系雅可比Θ函在海森堡群之一离散子群作用下不变。见海森堡群之Θ表示一文。
推广若F为一n元二次型,则有一关连的Θ函数
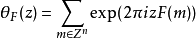 其中
其中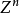 为整数格。此Θ函数是模群(或某适当子群)上的权n/2 模形式。在其富理埃级数
为整数格。此Θ函数是模群(或某适当子群)上的权n/2 模形式。在其富理埃级数
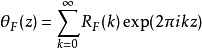 中,
中,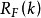 称为此模形式之“表示数”(representation numbers)。
称为此模形式之“表示数”(representation numbers)。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国