[科普中国]-艾森斯坦级数

在数学中，艾森斯坦级数是一类可直接表成级数的模形式，由费迪南·艾森斯坦首创。对于一般的约化群，罗伯特·朗兰兹也发展了相应的理论。1

模群的艾森斯坦级数固定整数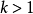 ，对上半平面上的复数 ，定义艾森斯坦级数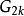 为：

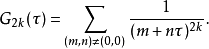此级数是上半平面上的全纯函数，此外它更是模群 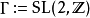的权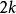 模形式。换言之，若 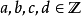满足 ，则

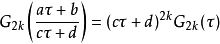
递回关系模形式理论中的一个基本事实是：模群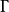 的模形式俱可表为 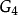与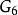 的多项式。作为特例，以下说明如何将艾森斯坦级数递回地表成 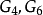的多项式。2

置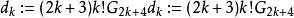 ，遂有下述关系式：

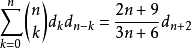在此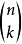 是二项式系数而 。

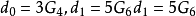函数 可以表示魏尔斯特拉斯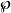 函数：

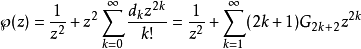
傅立叶展开置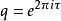 ，由于艾森斯坦级数是模群的模形式，故有傅立叶展开式：3

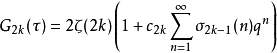
其中的傅立叶系数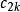 是

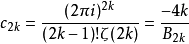此处的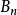 是伯努利数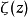， 是黎曼ζ函数，而 是n的正因数的p次幂和。

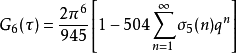
当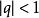 ，对q之和亦可化成兰伯特级数

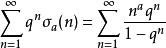有时也会考虑常数项等于一的艾森斯坦级数：

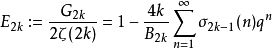
拉马努金公式拉马努金给出了许多有趣的艾森斯坦级数关系式，定义：4

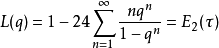
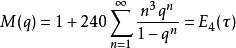
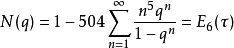
则有：

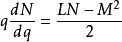
本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学