[科普中国]-范德华方程式

范德华方程（van der Waals equation）（一译范德瓦耳斯方程），简称范氏方程，是荷兰物理学家范德华于1873年提出的一种实际气体状态方程。范氏方程是对理想气体状态方程的一种改进，特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来，以便更好地描述气体的宏观物理性质。

简介范德华方程（van der Waals equation）（一译范德瓦耳斯方程），简称范氏方程，是荷兰物理学家范德华于1873年提出的一种实际气体状态方程。范氏方程是对理想气体状态方程的一种改进，特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来，以便更好地描述气体的宏观物理性质。1

方程的形式范德华方程具体形式为：

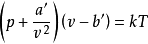式中p为气体的压强，a'为度量分子间引力的唯象参数，b'为单个分子本身包含的体积，v为每个分子平均占有的空间大小（即气体的体积除以总分子数量），k为玻尔兹曼常数，T绝对温度。1

适用范围范氏方程对气-液临界温度以上流体性质的描写优于理想气体方程。对温度稍低于临界温度的液体和低压气体也有较合理的描述。

但是，当描述对象处于状态参量空间(P,V,T)中气液相变区（即正在发生气液转变）时，对于固定的温度，气相的压强恒为所在温度下的饱和蒸气压，即不再随体积V（严格地说应该是单位质量气体占用的体积，即比容）变化而变化，所以这种情况下范氏方程不再适用。1

参见状态方程

气体定律

范德华常数表

范德华力

范德华半径

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学