在线性代数中,凯莱-哈密顿定理(Cayley–Hamilton theorem)(以数学家阿瑟·凯莱与威廉·卢云·哈密顿命名)表明每个布于任何交换环上的实或复方阵都满足其特征方程式。
定义明确地说:设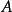 为给定的
为给定的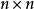 矩阵,并设
矩阵,并设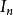 为
为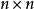 单位矩阵,则
单位矩阵,则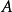 的特征多项式定义为:
的特征多项式定义为:
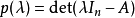
其中 det 表行列式函数。凯莱-哈密顿定理断言:
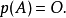
凯莱-哈密顿定理等价于方阵的特征多项式会被其极小多项式整除,这在寻找若尔当标准形时特别有用。
例子举例明之,考虑下述方阵:
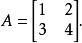
其特征多项式为
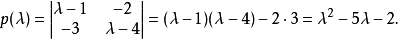
此时可以直接验证凯莱-哈密顿定理1:
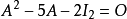
此式可以简化高次幂的运算,关键在于下述关系:
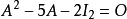
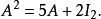
例如,为了计算{\displaystyle A^{4}},可以反复利用上述关系式:
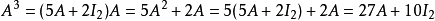
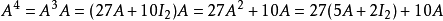

或是,如果要计算 ,也可以假设:
,也可以假设:
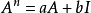
然后,依照前面的特征多项式之两解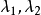 ,代入后可以得到
,代入后可以得到
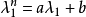
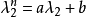
然后解方程后求出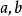 ,便可得
,便可得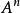 .
.
此外,凯莱-哈密顿定理也是计算特征向量的重要工具。
注:一般而言,若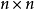 矩阵
矩阵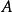 可逆(即:
可逆(即: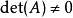 ),则
),则 可以写成
可以写成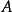 的幂次和:特征多项式有如下形式
的幂次和:特征多项式有如下形式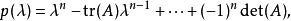
将方程式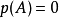 同乘以
同乘以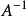 ,便得到
,便得到
定理证明以下考虑布于域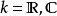 上的矩阵2。
上的矩阵2。
凯莱-哈密顿定理可以视为线性代数中拉普拉斯展开的推论。拉普拉斯展开可推出若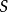 是
是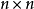 矩阵,而
矩阵,而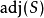 表其伴随矩阵,则
表其伴随矩阵,则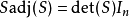
 取
取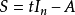 ,便得到
,便得到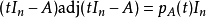 。此式对所有
。此式对所有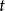 皆成立,由于实数或复数域有无穷多元素,上式等式在多项式环内成立。
皆成立,由于实数或复数域有无穷多元素,上式等式在多项式环内成立。
设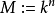 ,矩阵
,矩阵 赋予
赋予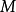 一个
一个 -模结构:
-模结构: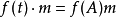 。考虑
。考虑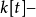 模
模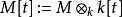 ,我们有
,我们有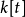 -模之间的“求值态射”:
-模之间的“求值态射”:

固定 ,对
,对 中的等式
中的等式
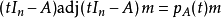
右侧取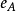 后得到
后得到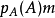 ,左侧取
,左侧取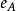 后得到
后得到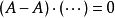 。明所欲证。
。明所欲证。
一个简单的证明: 令:
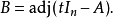
由: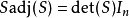
得:
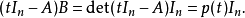

因两多项式,他们的对应项系数相等得:
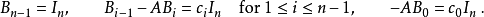
在等式两边t的i次项系数分别乘以A, 并将等式左右两边分别相加并合项得:
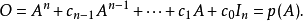
得证.
抽象化与推广前述证明用到系数在 的矩阵的克莱姆法则,事实上该法则可施于任何系数在交换环上的矩阵。借此,凯莱-哈密顿定理可以推广到一个交换环
的矩阵的克莱姆法则,事实上该法则可施于任何系数在交换环上的矩阵。借此,凯莱-哈密顿定理可以推广到一个交换环  上的任何有限生成自由模
上的任何有限生成自由模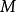 (向量空间是特例)。中山正引理的一种证明就用到这个技巧。
(向量空间是特例)。中山正引理的一种证明就用到这个技巧。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国