[科普中国]-超越运算

**超运算（或称为超越运算）**一般来说指的是超运算序列（数学中一种二元运算的序列）的前三项分别为加法、乘法、幂，除了序列中第一项的加法运算之外，序列中每一项的运算都是重复的前一项的运算。

定义超运算序列是定义在自然数集上的一个序列，记为。前几项为加法（n=1）、乘法（n=2）和幂（n=3）。高阶超运算的参数与幂运算相似，即a称为底数，b称为指数（或称超指数），而n则称为阶数。

用高德纳箭号表示法可以将超运算定义为

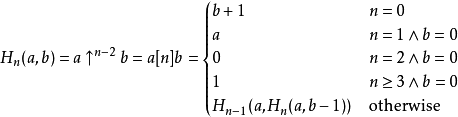
注意到，对于序列的前三项有：

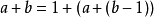
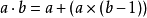
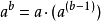通过这样的递归能够定义出高阶运算，从而输入很小的数就可以产生非常大的数。1

其实，某一超运算就是一种基于低一阶超运算而进行数的复合的方法。我们可以以加法、乘法与幂的概念为例来说明。加法运算就是将指定次数的1加到原本的数上从而得到最终的结果（如2+3是将1三次加到2上），乘法运算就是将指定次数的某数通加（如就是3个2相加），幂运算则是将指定次数的某数通乘（如就是3个2相乘）。

历史1914年，阿尔伯特·贝内特（Albert Bennett）最早提出了超运算，他发展出了一套交换超运算（见下文）的理论。12年之后，威廉·阿克曼定义了函数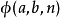，和超运算序列已经有了某种程度上的相似。最早的使用三个自变量的阿克曼函数使用了同样的递归法则，但有两点与现在的超运算不同。一是它定义了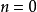时为加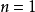法、时为乘法、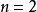时为幂运算，二是由其对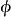初始条件的定义能得到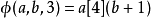，最后的运算结果与超运算不同。

1947年，鲁宾·古德斯坦提出现在所使用的超运算序列，只是那时他使用记号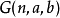来表示，而非今天的。在1947年的论文中，古德斯坦还引进了幂运算之后超运算的英文名称，即tetration、pentation、hexation等。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所