[科普中国]-彩虹表

彩虹表是一个用于加密散列函数逆运算的预先计算好的表, 为破解密码的散列值（或称哈希值、微缩图、摘要、指纹、哈希密文）而准备。一般主流的彩虹表都在100G以上。 这样的表常常用于恢复由有限集字符组成的固定长度的纯文本密码。这是空间/时间替换的典型实践, 比每一次尝试都计算哈希的暴力破解处理时间少而储存空间多，但却比简单的对每条输入散列翻查表的破解方式储存空间少而处理时间多。使用加salt的KDF函数可以使这种攻击难以实现。彩虹表是马丁·赫尔曼早期提出的简单算法的应用。1

背景为了保证后台数据安全,现在的做法都是使用哈希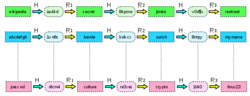算法对明文密码进行加密后存储。由于哈希算法不可逆向，因此由密码逆向出明文运算就成了不可能。

起初黑客们通过字典穷举的方法进行破解，这对简单的密码和简单的密码系统是可行的，但对于复杂的密码和密码系统，则会产生无穷大的字典。为了解决逆向破解的难题，黑客们就产生了彩虹表的技术。

为了减小规模太大的不足，黑客生成一个反查表仅存储一小部分哈希值，而每条哈希值可逆向产生一个密码长链（多个密码）。虽然在链表中反查单个密文时需要更多的计算时间，但反查表本身要小得多，因此可以存储更长密码的哈希值。Rainbow tables是此链条技术的一种改进，并提供一种对被称为“链碰撞”的问题的解决方案。其基于Martin Hellman理论(基于内存与时间的权重理论) 。

介绍为了解决简单的哈希链中的碰撞问题，彩虹表选用一系列相关的衰减函数R1，…，Rk来代替原先的衰减函数R。这样，如果两个哈希链发生碰撞并且重合，那么它们的碰撞必定发生在相同的位置，从而它们的终点也将相同。这样，我们可以通过后处理来对哈希链进行排序，从而找出并移除所有终点相同，因而可能是重复的链，并生成新的链来将整个表补充完整。这样得到的表中的链可能有碰撞的部分，但它们不会发生链的重合，从而大幅降低了碰撞的次数。2

采用衰减函数列代替衰减函数将改变查找的方式。因为给定的哈希值可能出现在哈希链中的任意位置，我们需要计算k条不同的链：首先假定给定的哈希值出现在哈希链的最后一位（此时我们只需施加函数Rk），然后假定哈希值出现在哈希链的倒数第二位（此时我们依次施加函数Rk-1，H和Rk），依此类推，直至我们找到所需的密码。注意，如果我们错误地假定了目标哈希值在哈希链中的位置，可能会得到一条与表中的链部分重合的链，从而产生误报。

计算过程假设我们有一个哈希方程H和一个有限的密码集合P。我们需要预先计算出一个数据结构来帮我们决定哈希方程H的任意一个输出结果h是否可以通过密码集合P里面的一个元素p经哈希函数H(p) =h得到。实现这一目的的最简单的方法是计算出P集合内所有密码p的哈希值H(p)。但是这个方法要求Θ(|P|n)，（n代表哈希函数H的一个输出值的大小，对于较大的|P|，n会变得过高)字节的空间来储存结果。

哈希链可以用来减少对于储存空间的需求。大致想法是通过定义一个归约函数（reduction function）R来影射散列值h在集合P中对应的密码p。（注意，这里的归约函数并不是真正意义上哈希函数的反函数。)然后通过用归约函数来替代哈希函数，形成交替的密码和哈希值。例如，如果P是6个字符的密码集合，而哈希值有32位长，那么他们形成的长链如下：

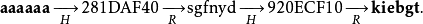
例子已知一个32位的哈希值 -〉 获得哈希值的最后4个字符。

对于归约函数的唯一要求是，它需要能返回特定字符的纯文本值。

为了生成查找表，我们从初始密码集合P中随机选择一个子集，对子集中的每个元素计算长度为k的哈希链，然后只保存每条哈希链的初始和末尾密码。我们把初始密码称为起点，把末尾密码称为终点。在上述哈希链的例子中，"aaaaaa"和"kiebgt"即为起点和终点，而哈希链中的其他密码或者哈希值均不会被保存。

现在，对于给定的哈希值h我们来计算它的逆（即找到对应的密码），从哈希值h开始，我们通过依次施加函数R和H生成一个哈希链。如果哈希链的任何节点与查找表的某个终点发生了碰撞，我们就可以找到与之对应的起点，然后用它重建对应的哈希链。而这个哈希链很可能包含了h，如果这样的话，那么它的前驱节点即为我们要寻找的密码p。

例如，如果给定的哈希值为920ECF10，我们首先施加函数R：

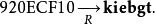因为"kiebgt"就是我们查找表的一个终点，所以我们找到对应的起始密码"aaaaaa"，然后搜索由它生成的哈希链直到找到920ECF10：

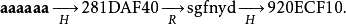因此，目标密码即为"sgfnyd"。

注意，这里的哈希链并不总是会包含我们要寻找的哈希值h；很可能以h开始的链会和起点在h链之后的某个查找链重合。例如，我们可以从FB107E70的哈希链中找到kiebgt：

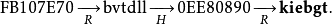
但FB107E70并不在以"aaaaaa"开头的链中。这种情况被称为误报。在这个例子中，我们可以忽略这个匹配然后继续扩增h链同时寻找下一个匹配。如果h的哈希链在扩增到长度为k后仍然没有发生匹配，那么与之对应的密码一定不在查找表的任何哈希链中。

查找表的内容并不依赖于查询的哈希值。它是在一次性建立之后，被无修改的重复用于查找。增加链的长度可以减小表的规模，但同时也会增加查询时间，这就是彩虹表空间换时间的折中策略。在单元链的最简单情况下，查询速度会非常快，但表也会非常大。一旦链变得更长，查找速度也会降下来，但表的规模变得更小了。

简单的哈希链方法有很多缺陷。最严重的问题是，如果两条链中的任何两个点碰撞（有同样的值）了，他们后续的所有点都将重合，这将导致在付出了同样的计算代价之后并不能使表尽可能多的覆盖到密码。由于链的前部并没有整个的保存，这使得碰撞不可能有效检测到。例如，如果链3的第三个值和链7的第二个值重合了，那么这两条链将覆盖几乎同样的值，但他们的终点值却不相同。哈希函数H本身不大可能产生碰撞，因为这就是它最重要的安全特性之一。但对于衰减函数R来说，由于他需要正确的覆盖掉可能的明文（即之前讨论的密码），所以不会是抗碰撞的。

其他的困难是由选择正确R函数的重要性导致的。选择恒等映射作为函数R要比暴力搜索好一点。只有当攻击者明确知道明文的可能取值是什么时，他/她才需要选择一个好的R函数使得时间和空间花费在这些可能的明文上，而不是整个可能的密文空间。尽管把R的取值限定到可能的明文空间能带来好处，但它的弊端是攻击者选择的用于生成哈希链的明文子集可能并不能覆盖所有的可能明文空间。设计一个能匹配明文期望分布的R函数也非常困难。

本词条内容贡献者为:

王慧维 - 副研究员 - 西南大学