[科普中国]-对数方程组

对数方程组(system of logarithmic equations)是一种常用的代数方程组，指由几个对数方程，或至少有一个对数方程和几个代数方程组成的方程组。解对数方程组的一般步骤是：1.把方程组中的对数方程化为代数方程；2.解代数方程组；3.验根1。

基本介绍对数方程组是指由几个对数方程，或至少有一个对数方程和几个代数方程组成的方程组。解对数方程组的方法主要是三种：

1) 利用对数方程的解法，“化去”底和对数符号，化为代数方程组。或用换元法把原方程组化为代数方程组。

2) 利用过去学过的方程组解法，如代入法、加减法，相乘或相除等消元，化为含有一个未知数的方程。

3) 将以上两种方法结合使用。

和解对数方程一样，要注意增根或遗根问题2。

例题解析【例1】解方程组：

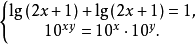
解：原方程组化为

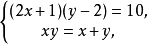解此方程组，得到

检验后知道，原方程的解为：

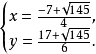
【例2】解方程组：

解：原方程组化为

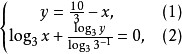(1)代入（2）：

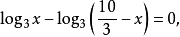解此方程得：

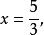将x的值代入（1）得

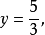经检验，原方程的解为

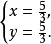
本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所