[科普中国]-近独立粒子统计力学

近独立粒子统计指的是统计力学中对粒子的特定描述，它的特点是不考虑粒子间的相互作用。

简介近独立粒子统计指的是统计力学中对粒子的特定描述，它的特点是不考虑粒子间的相互作用。近独立粒子三种主要模式是：

描述古典系统用：麦克斯韦-玻尔兹曼统计

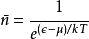
描述含费米子的量子系统用：费米-狄拉克统计

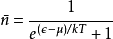
描述含玻色子的量子系统用：玻色-爱因斯坦统计

这三种统计的不同之处在于：

在古典物理中，粒子被视为能被区分出来的不同个体。

在量子物理中，两个费米子不能处于同一个物理态。

在量子物理中，要区分玻色子只能从不同的物理态入手，位处同一态的玻色子没有分别。因此，在物理态一的光子甲及在物理态二的光子乙，跟态一的光子甲及在态二的光子乙没有分别。但在古典物理中它们会是两个不同的系统，而在量子物理只算作一个。故玻色子表现得像它们都喜欢在同一状态似的。

数学上使用可交换算符描述玻色子，反交换算符描述费米子，所以造成了以上的差别。1

全同粒子在量子力学里，全同粒子是一群不可区分的粒子。全同粒子包括基本粒子，像电子、光子，也包括合成的粒子，像原子、分子。

全同粒子可以分为两种类型：

玻色子可以处于同样的量子态。光子、胶子、声子、与氦-4原子，都是玻色子。

费米子不能处于同样的量子态（这性质称为泡利不相容原理）。电子、中微子、夸克、质子、中子、氦-3原子，都是费米子。2

参阅全同粒子

盒中气体

费米气体

玻色气体

本词条内容贡献者为:

李晓林 - 教授 - 西南大学