[科普中国]-机率幅

在量子力学里，机率幅，又称为量子幅，是一个描述粒子的量子行为的复函数。例如，概率幅可以描述粒子的位置。

绪论在量子力学里，机率幅，又称为量子幅，是一个描述粒子的量子行为的复函数。例如，机率幅可以描述粒子的位置。当描述粒子的位置时，机率幅是一个波函数，表达为位置的函数。这波函数必须符合薛定谔方程。

描述一个机率幅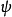 的概率密度函数是 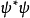，等于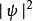 ，又称为概率密度。在使用前，不一定要将概率密度函数归一化。尚未归一化的概率密度函数可以给出关于概率的相对大小的信息。

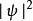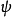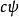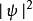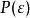假若，在整个三维空间内，概率密度 是一个有限积分。那么，可以计算一个归一常数 ，替代 为 ，使得有限积分等于1。这样，就可以将机率幅归一化。粒子存在于某一个特定区域V内的概率是 在区域V的积分。这句话的含义是，根据量子力学的哥本哈根诠释，假若，某一位观察者试着测量这粒子的位置。他找到粒子在 区域内的概率 是

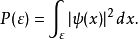
不光局限于粒子观，机率幅的绝对值平方可以诠释为“在某时间、某位置发生相互作用的概率”。1

概率流跳到导航跳到搜索

在量子力学里，概率流，又称为概率通量，是描述概率密度流动的物理量。假若将概率密度想像为非均匀流体。那么，概率流就是这流体的流率（概率密度乘以速度）。

在量子力学里，从概率守恒可以得到“概率连续性方程”。设定一个量子系统的波函数为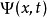 。定义概率流J为

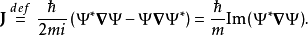其中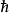， 是约化普朗克常数，m是质量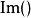，是取括弧内项目的复值。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所