[科普中国]-高次同余方程

高次同余方程(congruence equation of higher degree)是初等数论中的一个概念，是一类同余方程，它是关于未知数的n(n>1)次多项式的同余方程。

基本介绍设整数m>1，n>0，整系数多项式

f(x)=anxn+an-1xn-1+…+a1x+a0，an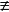0(mod m)，

同余式

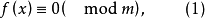称为n次同余方程，式中n称为方程(1)的次数，当n>1时，(1)称为高次同余方程。如果x0满足f(x0)≡0(mod m)，则x≡x0(mod m)称为同余方程(1)的解，不同的解是指对模m互不同余的解。当同余方程(1)的首项系数an>1时，总可以用an的数论倒数an′(即an′an≡1(mod m))去乘方程(1)的各项，将首项系数化为1，因此，研究高次同余方程时，常设an=1。若模m的标准分解式为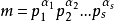，则方程(1)和下面方程组

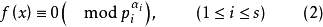等价，且方程(1)的解数为方程组(2)中各个方程的解数之积。所以，讨论方程(1)的解法，都可转化为研究首项系数为1，模为素数p的高次同余方程的解法问题1。

相关定理定理1 设m= m₁，m₂，...，mk，其中m₁，m₂，...，mk是k个两两互素的正整数，f(x)是整系数多项式，以T与Ti(1≤i≤k)分别表示同余方程

f(x) ≡0( mod m) (1)

与

f(x) ≡ 0(mod mi) (2)

的解的个数，则(1)和(2)是等价的，它们的解和解数相同，且T= T₁T₂...Tk2。

任一正整数m可以写成标准分解式：即

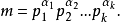
由定理1知，欲解同余方程f(x) ≡0( mod m),只要解同余方程组

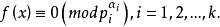下面就来讨论

f(x)≡0(mod pα)，p为素数 (3)

的解法。适合(3)的每一个整数都适合同余方程

f(x)≡0(mod p)， （4）

因此欲求（3），可以从（4）式出发2。

定理2 设x≡x₁(mod p)即

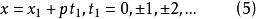是(4)的一个解，且p∤f'(x1)(f'(x)是f(x)的导函数)，则(5)刚好给出(3)的一个解(对模pα来说):

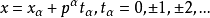即x≡xα(mod pα)，其中xα≡x1(mod p)。

推论 在定理2 的符号和条件下，设c是

f(x)≡0(mod p)， （4）

的解，且p∤f'(c)，那么，对任意的α≥2，同余方程(3)满足条件x≡c(mod pα-1)的解数均为1。特别，当同余方程(4)与同余方程x≡c(mod pα-1)无公共解时，同余方程(4)对任意的α≥1解数均相同2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所