[科普中国]-绝对假素数

绝对假素数(absolute improper prime number)亦称绝对伪素数，是一类特殊的合数，指对一切整数a，满足n|(an-a)的合数n，由定义知合数n应能整除2n-2，3n-3，4n-4，…，即使a为负整数，n|(an-a)也能成立。从费马定理可以证明561能整除a561-a，又因561=3·11·17，所以561是绝对假素数。已知的绝对假素数还有：2 821，10 585，15 841，至今还不知道是否存在无穷多的绝对假素数1。

基本介绍整除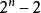 的合成数n是假素数，整除 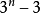或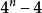 等等的合成数n，我们认为，也具有某种假素数的性质。一个合成数n如果整除 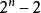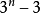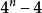， ， ，...以及对任何整数a，即使是负整数，也整除 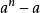，肯定是这方面最极端的情形，称为绝对假素数。

最小的一个绝对假素数是561，这就是说，561是一个合成数，而a561-a可以被561整除，不论a是什么整数。这是不难证明的，直接从费马小定理推出。

561的素因子分解是(3)(11)(17)，我们必须证明：a561-a可以被这三个素数的每一个整除。我们有

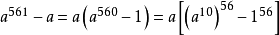
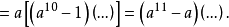
但是据费马定理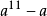， 可被11整除，因为11是素数，于是，11整除a561-a，同样可以证明3和17也都是因子。

另外几个绝对假素数是:

(1)2821=(7)(13)(31)；

(2)10585=(5)(29)(73)；

(3) 15841=(7)(31)(73)。
现在还不知道是否存在无限多的绝对假素数2。

相关介绍对于费尔马小定理的逆命题，一直研究了两千多年，直到1830年，一位不愿公开自已姓名的德国作者写了一篇文章，对这个命题予以否定。他的证明很简单，举出一个反例3：

当n=341时，

2341-2= 2(2340-1)，

2340-1含有210-1的因子，而

210-1= 1023=3×341。

∴2341-2能被341整除，

但341=11×31，它不是合数。

因此，费尔马小定理的逆命题是不成立的。

应当承认，能整除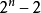 的n，绝大多数是素数，象341这样“鱼目混珠”的合数是极少数。数学家给它们起了一个古怪的名字一假素数，意思就是“冒牌的素数”。

1909年，巴拉切微兹证明了，在2000以内只有五个假素数：

341 = 11·31； 561 = 3·11·17；

1387 = 19·73； 1729= 7·13·19；

1905=3·5·127.

超过2000以上的假素数也陆续发现了一些，如：

2047 = 23·89； 2701 = 37·73；

4369=7·257； 4681= 31·151；

10261 = 31·331。

1950年，美国著名数论家拉美证明了

161038=2×73×1103。

可以证明， 这种假素数有无穷多个3。

数学家还研究了一种所谓的“绝对假素数"，设n是一个合数，n如果能够整除

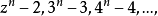n就叫做绝对假素数。人们找到最小的一个绝对假素数是561 = 3·11·17，它能整除 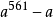，a为任何正整数。这种绝对假素数真是凤毛麟角。1978年，发现了第685个绝对假素数，它是当时所知道的最大的一个3：

443656337893445593609056001.

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所