[科普中国]-补二面角

补二面角(supplementary dihedral angle)是两个数量相关的二面角，指平面角互补的两个二面角，其中任一个二面角都称为另一个二面角的补二面角1。

基本介绍定义1 延长二面角的两个半平面，与原二面角的平面角不相邻的二面角称为原二面角的对顶二面角，与原二面角的平面角相邻的二面角称为原二面角的补二面角。

从定义知，二面角及其对顶二面角是其任一补二面角的补二面角2。

相关定理定理1 二面角的平面角与其对顶二面角的平面角相等，与其补二面角的平面角互补2。

定义2 把二面角的平面角二等分的半平面称为该二面角的内平分平面;把二面角其中-个补二面角的平面角二等分的半平面称为该二面角的外平分平面.

从定义2知，二面角的外平分平面是其对应补二面角的内平分平面。

定理2 二面角的内平分平面和其对应补二面角的外平分平面是唯一的。

证明 假设二面角的平面角是2α，二面角的内平分平面不是唯一的，还存在另一内平分平面，两内平分平面的二面角的平面角是β>α，因而其中一个内平分平面与二面角一半平面所得的二面角的平面角是α+β> 2α，与内平分平面的定义矛盾，所以二面角的内平分平面是唯一的。同理可证二面角其对应补二面角的外平分平面是唯一的。

我们容易得到

定理3 二面角的内平分平面与外平分平面互相垂直，二面角的内平分平面与其对顶二面角的内平分平面共面，两个外平分平面共面。

定理4 一个半平面是二面角的内平分平面的充要条件是该半平面上任意一点到二面角的两个面的距离相等。

证明 充分性

如图2，设A是平面γ内的一点，AB⊥α,AC⊥β，垂足分别是B和C，AB= AC，如果点A在二面角α-a-β的棱a上，则结论成立，如果点A不在a上，作BD⊥a，与a相交于点D，连AD、CD。由前面的证明知道∠BDC是二面角α-a-B的平面角。又因为△ABD≌△ACD，所以∠ADB= ∠ADC，因此平而γ是二面角α-a-β的内平分平面。

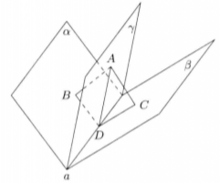
必要性

在二面角α-a-β的内平分平面γ内取-点A,，如果点A在a上，那幺结论成立。如果点A不在a上，作AB⊥α，AC⊥β，垂足分别是B和C，做BD⊥a，与a相交于点D，连AD、CD。因为AB⊥α，AC⊥β。所以AB⊥a，AC⊥a，即a⊥平面ABC。又因为BD⊥a，所以a⊥平面ABD，由于过点A且与a垂直的平面只有一个，所以A、B、C、D共面，于是得CD⊥a，所以∠BDC是二面角α-a-β的平面角，因此∠ADB=∠ADC，于是△ABD≌△ACD，所以AB= AC2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所