空间旋转反射(rotation reflection in space)是一种空间变换,如果f₁=ω(a,φ)是空间的一个旋转角为φ的旋转变换,a为旋转轴,f₂是空间的一个面反射变换,反射面为α,当a⊥α时,变换积f₂·f₁称为空间的旋转反射变换;并且直线a称为旋转反射轴,α称为旋转反射面,a和α的交点O称为旋转反射心,φ称为旋转反射角。空间中三个面反射的积,当三个反射面恰有一个公共点时,就可以化为一个旋转反射,其公共点就是旋转反射心。旋转反射属于第二种合同变换,空间点反射是旋转角为二直角时的旋转反射,空间面反射是旋转角为零的旋转反射1。
基本介绍空间旋转反射是指空间的旋转反射变换,空间的旋转反射与空间的面反射变换的乘积称为空间的旋转反射(变换),此变换属于第二类合同变换1。
空间旋转变换是一种特殊的几何变换,指空间的所有点绕同一直线旋转同一角度的变换。旋转变换简称旋转,是欧氏几何中的一种重要变换,即在欧氏平面上(欧氏空间中),让每一点P绕一固定点(固定轴线)旋转一个定角,变成另一点P′,如此产生的变换称为平面上(空间中)的旋转变换,此固定点(固定直线)称为旋转中心(旋转轴),该定角称为旋转角。旋转是第一种正交变换,在平面直角坐标系中,若旋转中心为点M0(x0,y0),点P(x,y)绕M0旋转定角θ后变成点P′(x′,y′),则平面上旋转变换的代数表达式为
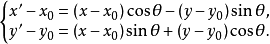
旋转变换的逆变换也是旋转变换,两个绕同一点(同一轴线)的旋转变换的乘积仍是旋转变换,所有绕同一点(同一轴线)的旋转变换的全体构成一个群,称为旋转群,在旋转变换下,两点间的距离与两直线的交角均保持不变,旋转变换的概念可以推广到n维欧氏空间。绕O(0,0,…,0)点旋转的代数表达式为
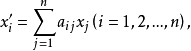 或用矩阵表示为:(x′i)=(aij)·(xi),其中aij为常数,且(x′i),(xi)均为n×1矩阵,矩阵(aij)是行列式等于1的正交矩阵。
或用矩阵表示为:(x′i)=(aij)·(xi),其中aij为常数,且(x′i),(xi)均为n×1矩阵,矩阵(aij)是行列式等于1的正交矩阵。
镜面反射变换简称镜面反射或平面反射,欧氏空间中的一种特殊变换。在欧氏空间中,把任一点A映成关于给定平面π对称的点A′的变换称为关于平面π的镜面反射变换,平面π称为反射平面。镜面反射是第二种正交变换。在镜面反射变换下,连结变换的每一对对应点A,A′所得到的线段都垂直于反射平面π且被π所平分,平面π上的点都是不动点,镜面反射变换在直观上相当于把平面π看做一面镜子,变换前后的对应点就好比是物与像那样,在空间直角坐标系中,若把坐标平面xOy取为反射平面,则镜面反射变换的代数表达式为
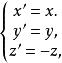 其中(x,y,z),(x′,y′,z′)分别是变换前的点与变换后它的对应点的坐标1。
其中(x,y,z),(x′,y′,z′)分别是变换前的点与变换后它的对应点的坐标1。
相关介绍如果一个图形F在合同变换f下对应于图形F',那么称图形F与F'合同。
我们不难发现,合同变换下,两个对应图形F与F'的边界方向(顺时针方向或逆时针方向)或者是一致的,或者是反向的。因此,按照对应图形的边
界方向可以将合同变换分为两类:将使得对应图形F与F'的边界方向相同的合同变换称为第一类合同变换(如图1),而将使得两个对应图形F与F’边界方向相反的合同变换称为第二类合同变换(如图2)。因而,我们将在第一类合同变换下的对应图形F与F‘称为真正合同,而把第二类合同变换下的对应图形F与F'称为镜像合同2。
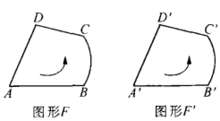
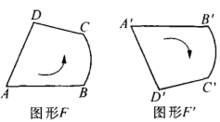
利用上述分类方式,我们容易得到,平移变换、旋转变换(即两个反射变换的乘积)是第一类合同变换,而反射变换是第二类合同变换。
既然平移变换、旋转变换是两个反射变换的乘积变换,那么(自然的思考),合同变换是否也是几个反射变换的乘积变换呢?
我们猜测并可以证明:
性质1 任一合同变换至多可以表示为三个反射变换的乘积2。
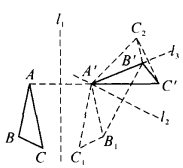
证明 设合同变换ω由三对不共线的对应点A与A',B与B',C与C'所确定(图3)。
作AA’的垂直平分线 ,那么,在以
,那么,在以 为反射轴的反射变换下,△ABC变为△A'B₁C₁(若点A与A'重合,则没有必要施行
为反射轴的反射变换下,△ABC变为△A'B₁C₁(若点A与A'重合,则没有必要施行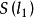 )。此时,AB=A'B₁=A'B'。
)。此时,AB=A'B₁=A'B'。
再作线段B₁B'的垂直平分线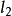 ,则点A'必在
,则点A'必在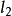 上,以
上,以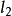 为反射轴的反射变换
为反射轴的反射变换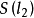 将△A'B₁C₁
将△A'B₁C₁
变为△A'B'C₂(如果B₁与B'重合,也没有必要施行变换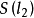 。此时A'C'=AC=A'C₁=A'C₂,B'C'=BC=B₁C₁=B'C₂。
。此时A'C'=AC=A'C₁=A'C₂,B'C'=BC=B₁C₁=B'C₂。
最后作线段C'C₂的垂直平分线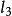 ,点A'、B'必在直线
,点A'、B'必在直线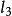 上。在反射变换
上。在反射变换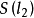 的作用下,△A'B'C₂变为△A'B'C'(若点C'与C₂重合,则不必施行变换
的作用下,△A'B'C₂变为△A'B'C'(若点C'与C₂重合,则不必施行变换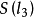 ,于是,
,于是,
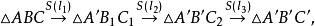 即
即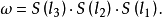
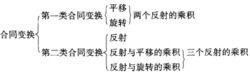
综上所述,对于第一类合同变换,总可以表示为两个反射变换的乘积;对于第二类合同变换,总可以表示为一个反射变换或三个反射变换的乘积,于是得下表2:
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国