[科普中国]-格雷贝作图法

格雷贝作图法(Grebe construction method)是求作三角形的陪位重心的一种方法。自三角形△ABC各边向外作正方形得正方形BCPP′，CAQQ′和ABRR′，设QQ′与RR′，RR′与PP′，PP′与QQ′分别交于点X，Y，Z，则AX，BY，CZ三直线交于△ABC的陪位重心。用这个方法来求作三角形的陪位重心称为格雷贝作图法1。

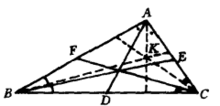
基本介绍三角形每条中线的等角线叫做陪位中线或类似中线，三条陪位中线的交点，即重心的等角共轭点，叫做陪位重心或类似重心。图中AD、BE、CF是三角形ABC的三条中线，AK、BK、CK是陪位中线，K点是陪位重心2。

格雷贝作图法 如图2，在△ABC的外边作正方形BCPP'、CAQQ'、ABRR'，设QQ'与RR’、RR'与PP'、 PP'与QQ' 的交点各为X、Y、Z，则AX、BY、CZ三线会于△ABC的陪位重心，按此法求三角形的陪位重心，称为格雷贝(Grebe)作图法2。

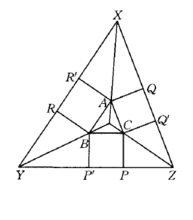
格雷贝作图法的证明在△ABC三边上向外作正方形ABEF，BCXY，CANM，如图3。

(1)过点A作AH⊥FN，H为垂足，AH交BC于点G，如图3，则BG= CC。

(2)设EF分别与MN和XY相交于点D和P，MN和XY相交于点Q，则DA，BP，CQ都过△ABC的陪位垂心3。

提示 (1)过B和C两点作BS⊥AG⊥CR，S和R为垂足，如图3.

证Rt△AHF≌Rt△BSA和Rt△AHN≌Rt△CRA，...。

(2)证A，F，D，N四点共圆，....，由(1)知AG是BC边上的中线，设AD交BC于点Z，证∠BAZ=∠GAC，即AZ是△ABC边BC上中线AG的陪位中线，...3。

格雷贝三角形自三角形各边向外作正方形，延长与三角形三边相对的正方形边长，所围成的三角形，称为外格雷贝(Grebe)三角形，如图44。

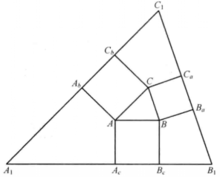
与上述作法完全相似，只不过三个正方形是向形内所作出的，这样得出的三角形称为内格雷贝三角形，如图5。

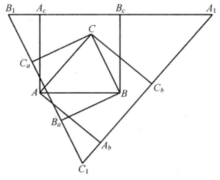
外、内格贝格三角形有丰富的性质，特别是与近百个三角形位似或透视，下面仅举数例。

(1) 外格雷贝三角形与下列三角形位似：△ABC；中点三角形；反补三角形；外心的垂足三角形；垂心的反垂足三角形；外心的外接切瓦三角形；欧拉三角形；约翰逊三角形。

(2) 外格雷贝三角形与下列三角形透视：垂足三角形；等角中线三角形；外心的反切瓦三角形；切线三角形；垂足三角形；外心的反垂足三角形；内肯姆塔点的反垂足三角形；共轭重心的外接切瓦三角形；反射三角形；第二勃罗卡三角形。

(3) 内格雷贝三角形与下列三角形位似：△ABC；中点三角形；反补三角形；外心的垂足三角形；垂心的反垂足三角形；外心的外接切瓦三角形；欧拉三角形；约翰逊三角形。

(4) 内格雷贝三角形与下列三角形透视：垂足三角形；等角中线三角形；外心的反切瓦三角形；切线三角形；垂足三角形；外心的反垂足三角形；共轭重心的外接切瓦三角形；反射三角形；第二勃罗卡三角形；外肯姆塔点的反垂足三角形4。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所