[科普中国]-夏农–菲诺–以利亚码

在消息理论中，夏农–菲诺–以利亚码是算术编码的先导，其机率被用于决定码字。1

算法描述给定一离散随机变数 ，令 为 发生之机率。

定义

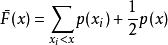
算法如下：

对每个X中的x,

令Z为 之二次展开

令x之编码长度

选定x之编码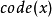， 为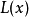 在Z之小数点后之第一个最高有效位。

算法举例令 X = {A, B, C, D} ，其发生机率分别为 p = {1/3, 1/4, 1/6, 1/4} 。

（1）对于 A

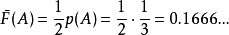
在二进制中， Z(A) = 0.0010101010...

code(A) 为 001

（2）对于 B

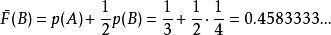
在二进制中， Z(B) = 0.01110101010101...

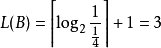
code(B) 为 011

（3）对于 C

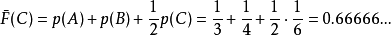
在二进制中， Z(C) = 0.101010101010...

code(C) 为 1010

（4）对于 D

在二进制中， Z(D) = 0.111

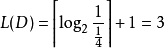
code(D) 为 111

算法分析前缀码夏农–菲诺–以利亚码之输出为二进制前缀码，因此可被直接解码。

令 bcode(x) 为二进制表示法最左侧加入小数点而成之小数。举例而言， code(C)=1010 ，则 bcode(C) = 0.1010 。 对所有 x ，如果没有任何 y 存在使得

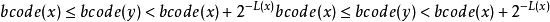
则所有的码可构成前缀码。

此性质可透过比较 F 和 X 之累积分布函数，以图1表示出：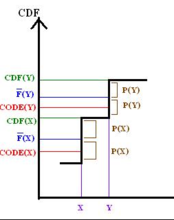

由 L 之定义可得

并且由于 code(y) 是由 F(y) 从 L(y) 之后的位元截短而得，故

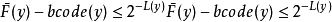
因此 bcode(y) 必不比 CDF(x) 小。

上图说明了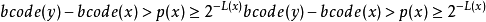 ，因此前缀码定理成立。

编码长度此码之平均长度为 。
因随机变数 X 之熵H(X) 满足

夏农–菲诺–以利亚码之长度约比代编码资料之熵长约一到二额外位元，故甚少被实用。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所