[科普中国]-对顶圆锥

对顶圆锥(vertically opposite circular cone)是一个圆锥形的几何体，用垂直于圆锥面的轴的两个平面去截圆锥面，如果圆锥顶点位于此两平行平面之间，两截口圆面与锥面围成的封闭几何体称为对顶圆锥。对顶圆锥是特殊的第二型截锥1。

基本介绍解析几何指出：用平面去截对称的对顶圆锥，平面和圆锥侧面相交的曲线统称为圆锥曲线。圆锥曲线是二元二次代数方程的解析式——ax²+bxy+cy²+dx+ey+f=0的几何化。对于任意一个二元二次方程，都有一条圆锥曲线与之对应，反之，对于任意一条圆锥曲线，也必然有一个二元二次方程作为它的解析式。圆锥曲线的变化，反映着二元二次方程的变化，反之亦然。那么圆锥曲线是怎样变化的呢?我们分两种情形来说明。

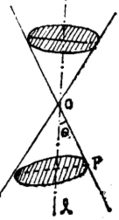
首先，平面经过圆锥顶点O，并且和中轴l垂直，这时其交线变为一点，若平面绕顶点逆时针旋转，随着旋转的量变积累，其与原平面的二面角等于90°—θ时，平面与圆锥侧面相交成为直线(即圆锥的侧棱)，这便是量变引起的质变了。过了这个关节点，即二面角大于90°—θ时，其交线变为相交于圆锥顶点的两条直线了。在这里又是一次渐进过程的中断——飞跃。 平面继续旋转直至180°时，交线的变化又依次为一条直线，一点。

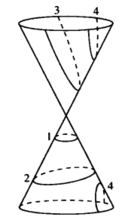
其次，平面不经过圆锥顶点，而与其相交于任意点P，且平面与轴l垂直，此时交线是一个圆。 平面绕P点逆时针旋转，交线便由圆转化为椭圆，发生了质变。随着旋转的量的增加，共与原平面的二面角等于90°一θ时，椭圆又质变为抛物线了。过了这个关节点，即二面角大于90°—θ时，其交线又变为双曲线了。平面继续旋转并达到180°的过程中，这种量变质变又会按颠倒了的次序重演。

曲线形式(第一种情形所得各种点、线，是圆锥曲线的特例)的量变质变，表现在描述曲线的方程上，就是二次曲线方程离心率e的量变质变2。

具体情况分析(一)、若一截面仅平行于圆锥的一条母线，则截面与圆锥面的截线为抛物线。

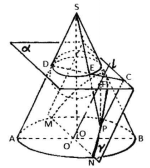
如图3，设有圆锥S-AB，平面γ //母线SA，交圆锥底面于MN，MN⊥AB。设P为平面γ与圆锥面截线上任一点。作圆锥S的一个内切球，内切球与圆锥面的切点圆平面为α，平面α与平面γ的交线为直线l，内切球切平面γ于F，连PF。

因平面α//圆锥底面，所以直线l//圆锥底面，所以MN//直线l，又MN⊥母线SA，所以SA⊥直线l。 过P作PC//SA，因SA//平面γ，所以PC 在平面γ内，所以PC⊥直线l。又设SA交平面α于D，连C、D交SP于E，因E在平面α内，又在圆锥母线SP上，所以E必在内切球与圆锥相切的切点圆上3。

由PC//SD，△SDE∽△PCE因SD=SE，所以PC=PE又PE、PF同为内切球的两切线，所以PF=PE，所以PC=PF，所以P 点的轨迹是以F为焦点、以直线l为准线的抛物线。

(二)、若一截面不过圆锥顶点而与圆锥面的所有母线都相交，则截面与圆锥面的截线为椭圆。(当截面与圆锥的轴垂直时，截线为圆)

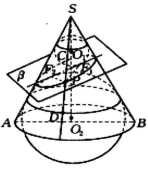
如图4，设有圆锥S-AB，平面β斜交圆锥所有母线，P为平面β与圆锥面的截线上任一点。 在圆锥内部、平面β两侧各作一内切球O₁和内切球O₂，使与圆锥侧面及平面β相切，得两个切点圆及两切点F₁、F₂。设母线SP交内切球O₁的切点圆于C，交内切球O₂的切点圆于D，连PF₁、PF₂。因PF₁、PC同为过P点的内切球O₁的两条切线，PF₂、 PD同为过P点内切球O₂的两条切线，

∴PF₁= PC，PF₂= PD，PF₁+PF₂=PC+PD=CD=定长，

∴P点的轨迹是以F₁、F₂为两焦点、以CD为长轴长的椭圆3。

(三)、若一截面不过圆锥顶点，且同时与圆锥面及其对顶圆锥面都相交，则截面与圆锥面的截线为双曲线。(截面与两母线平行)

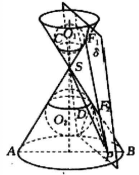
如图5，设有圆锥S-AB，平面δ同时与圆锥S-AB及对顶圆锥面都相交，P为相交截线上任一点。在对顶圆锥内分别作内切球O₁、内切球O₂与圆锥面及平面δ都相切，分别得两个切点圆及切点F₁、F₂，连PF₁、PF₂。又设母线PS分别交内切球O₁、内切球O₂于C、D。

因PF₁、PC同为过P点的内切球O₁的切线，PF₂、PD同为过P点的内切球O₂的切线，

∴PF₁= PC，PF₂=PD，

∴PF₁-PF₂= PC- PD=CD=定长，

∴P点的轨迹是以F₁、F₂为两焦点，以CD为实轴长的双曲线。

现在，我们也能证明为什么球被阳光斜照后的影子是椭圆，为什么圆柱形玻璃杯中水被倾斜后液面成椭圆。

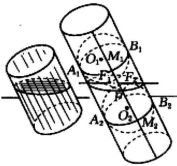
如图6，在圆柱内放进两个内切球O₁和内切球O₂，使与圆柱侧面及斜截面都相切，分别得切点圆O₁、切点圆O₂及两切点F₁、F₂。设P为圆柱斜截面交线上任一点，过P作圆柱母线，交两切点圆于M₁、M₂，

PM₁=PF₁，PM₂= PF₂，PF₁+PF₂= PM₁+ PM₂ = M₁M₂=定长，

∴P点的轨迹为以F、F为两焦点、长轴长为M₁M₂的椭圆3。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所