[科普中国]-正星体

正星体(regular star body)是一种特殊的正多面体，以正n面体各面为底，向外作正棱锥，使这些棱锥的侧面皆为相等的正三角形，这样得到的若是凹多面体，则称它为正(n角)星体。这类正星体有四种，它们分别是正六角星体、正八角星体(各有24个面)和正十二角星体、正二十角星体(各有60个面)1。

基本介绍正多面体中除了五种凸正多面体（又称“柏拉图立体”）外，还有四种正星体，它们是凹正多面体，开普勒（Kepler）与普安索(Poinsot)发现了这4种内凹的正多面体，故又把这四种正星体称为Kepler-Poinsot多面体。四种正星体分别是如图1至图4所示的正六角星体、正八角星体(各有24个面)和正十二角星体、正二十角星体(各有60个面)。

|| ||

开普勒与普安索的发现开普勒研究过正多面体(每个面皆为全等的正多边形的几何体)，他知道：早在古希腊时期，哲人柏拉图已发现了五种正多面体(正4、6、8、12、20面体，后来人们发现：凸正多面体仅有上面五种)，对于非凸的情形又将如何?

首先，开普勒（Kepler）发现了两种各面均为全等三角形的凹正多面体：小星状正十二面体和大星状正十二面体。1809年波因素特(Poinsot)（即普安索）又发现了两种凹正多面体(每面皆为全等三角形)：大十二面体和大二十面体。

附记 开普勒在研究天体运动时，还涉及了一些数学特别是几何问题。1611年他曾断言：在一个大立方体中堆放半径一样的小球，小球总体积与立方体积之比ρ不超过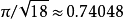(开普勒猜想)。这是一个至今尚未解决(证明)的结论，尽管人们对它的正确性并不怀疑，尽管人们对比值ρ不断改进，到目前为止，人们证明的最好结果是ρ≤0.7731，这是由数学家穆德(D.J.Muder)于1993年给出的2。

四种正星体的介绍小星状正十二面体正二十面体同一面的五个相邻面延展后，交于一点，与底面形成正五棱锥(图5)。类似的作法，其他十一个面上都会形成全等的正五棱锥。这种含十二个正五棱锥的星体称为小星状正十二面体(Small Stellated Dodecahedron)，它的直观图如图版6左，平面图如图版6右。其面数，顶点数，棱数分别为f=12,v=12,e=30。

这一星体作法的等价说法是：延展正十二面体各面所在平面(图版6左)，十二平面两两相交，形成十二个五角星形，正十二面体同一面上也同样出现十二个正五棱锥3。

大正十二面星体星体构造法减法中从正二十面体十二个对顶面使两两相交，相交面的公共部分出现一个凹多面体，这个立体就是第二种开普勒一普安索体。不妨设想在图7中正二十面体的D点有五条棱通过：DA、DE、DI、DH、DC。AEIHC为一平面正五边形，是正二十面体一个对顶面。除了对顶面LGBFJ与它平行外，其余十个对顶面与它两两相交，形成了一朵美丽的立体五角星(图8)。十二个对顶面上都出现了同样的立体，它们的全体就构成了大正十二面星体(Great Dodecahedron)。其面数，棱数，顶点数分别为12,30,12。其面数，顶点数，棱数分别为f=12,v=12,e=30。

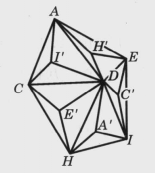
之所以称为十二面是因为它的十二个角顶分别对应一个正五角星形对顶面，它的直观图如图版9左，平面图为图版9右，它是小星状十二面体的对偶图形3。

大星状正十二面体大星状正十二面体是从大正十二面星体经过加法构造出来的。就在大正十二面星体外添加了二十个正三棱锥，它们的全体就是大星状正十二面星体(Great Stellated Dodecahedron)。之所以称为大星状正十二面星体是因为它有十二个面。其面数，顶点数，棱数分别为f=12,v=20,e=32。

大星状正十二面体作法的等价说法是：从大正十二面星体做加法，延展它的十二个面，使两两相交，在形外产生二十个正五棱锥，在同一延展面上的五边形扩展成正五角星，从此也就轻便地获知大星状正十二面体上每一正五棱锥的侧面也是以底角72。、顶角36。形成的等腰三角形。

另一方面，我们还有兴趣地看到，大星状正十二面体的核心恰是一个以它的正三棱锥底棱作为棱的正二十面体。因此它的模型是很容易制作的。

大正二十面星体大正二十面星体是从正二十面体的二十个面延展构成的。构造设想十分奇巧。其面数，顶点数，棱数分别为f=20,v=12,e=303。

本词条内容贡献者为:

王伟 - 副教授 - 上海交通大学