[科普中国]-球台

球台是球带和截得它的两个截面所围成的几何体叫做球台，球带的高叫做球台的高，两个截面叫做球台的底面。球台也可以看成是一个球被两个平行平面所截，两个截面之间所夹的球的部分1。

基本介绍球台的定义：（1）球台是球在与球相交的两个平行平面之间的部分。这些平面可以与球面相截，也可以相切。两平行平面所得截面一两个圆，称为球台的底面；两底面中心的连线，称为高。球台的侧面，称为球带。当两平行平面之一为切面时，则形成单底球台——球缺。当球台的高为球的直径时，即为全球2。（2）用两个平行平面去截球体，它们之间所夹的球体的部分，两个截面间的距离叫做球台的高；两个截面叫做球台的底面1。（3）球台也可以看作由圆弧和线段组成的曲边图形(如图2中的阴影部分)绕圆弧所在的圆的直径旋转而成的3。

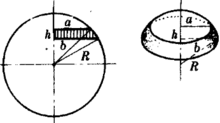
球台的相关计算

|| ||

半径为R的球的球台，如果上底半径为r1，下底半径为r2，高为h，则按底面在球心两侧或同侧面有如下两个关系式4：

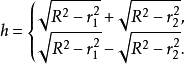
球台的体积为

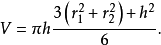
例 地球半径为R，北回归线的纬度是北纬23.5°，北极圈的纬度是北纬66.5°，试求以北回归线所在圆面和北极圈所在圆面为两底面的球台的高1。

解 球台的高h=R(1-sin23.5°)-R(1-sin66.5°)

=R(sin66.5°-sin23.5°)

本词条内容贡献者为:

王伟 - 副教授 - 上海交通大学