阿尔哈逊问题二(Alhazen problem Ⅱ)一般简称阿尔哈逊问题,是与圆有关的极值问题。若P为已知圆周上一动点,A,B为二定点,问P位于何处,可使:1.PA²+PB²,2.PA+PB为极大或极小1。
基本介绍阿尔哈逊问题二简称阿尔哈逊问题(Alhazen’s problem)也被称为阿尔哈森问题、阿尔哈岑问题、打子弹问题、Alhazen子弹问题等,指在平面上给定两个点,要在给定的圆周上求一个点,使得它到所给两个点的距离之和为最大或最小。这是阿拉伯物理学家兼数学家阿尔哈森(Alhazen,生年不详,殁于1039年)在其巨著《光学集锦》(Kitab al-manazer)中所提出的问题2。
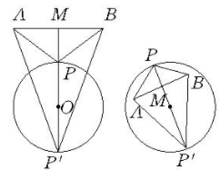

相关介绍“打弹子问题”这个数学名题,都说是阿拉伯数学家阿尔哈岑( al-Haitam Alhazen,约965~1039)首先提出来的其实,这个问题的实质性内容确是阿尔哈岑提出的,但“打弹子”的形式是后来人加上去的3。
阿尔哈岑是阿拉伯穆斯林学者中很有影响的一个物理学家,出生在南伊拉克的巴士拉,擅长机械设计,曾宣称要制造一台调节尼罗河泛滥的机械,他对光学也很有研究,写过一本《光学》的著作,所谓“打弹子问题”就是这本书里提出来的,原文的叙述是这样的:“在一个球形凹面镜上找出一个点,使由一个已知点射来的光线被反射到另一个已知点去。”这是几何光学的问题,若抽象成一个数学题目,可这样表述:“在一个已知圆内,作出一个其两腰通过圆内两个已知点的等腰三角形。"后来的一系列著名数学家都参与这个问题的研究,大家发现,阿尔哈岑提出的问题可以用形象的打弹子形式来表达,这个源出光学的问题,就变成了“阿尔哈岑弹子问题”:
一张圆形弹子台上有两只弹子球,用什么方法打击一球,使其从弹子台橡皮边缘弹回时必定撞击另一个球?”
解决方法求解这个问题的关键是要利用光学上人射角等于反射角的原理。如图3,设圆O内有A、B两点,P为圆周上所要求的一点,以O为原点建立直角坐标系,设A、B的坐标分别为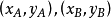 ,P的坐标为(x,y),只要P的坐标确定了,这个问题也就解决了3。
,P的坐标为(x,y),只要P的坐标确定了,这个问题也就解决了3。
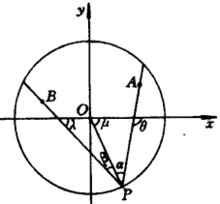
设PA、PO、PB与x轴的交角分别为θ、μ、λ,PA与PO、PB与PO的交角分别为α、β,根据光学反射定律,
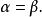
而α=θ-μ,β=μ-λ,
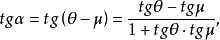
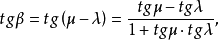 因为
因为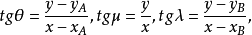
由 得
得
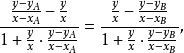 整理后,得
整理后,得
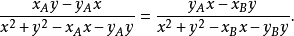 设
设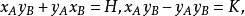
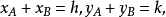 则最后可得
则最后可得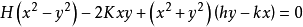 。
。
因为P(x,y)在圆O上,由圆的方程,可得
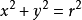 (r为半径).
(r为半径).
因此,上式可化为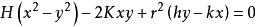 .
.
此方程代表一条双曲线,因此,最终答案是,所求P点由圆和双曲线的交点决定。由于一个圆和一条双曲线一般有四个交点,所求点P就可能有4个位置,这和由圆的方程与双曲线方程组成的二元二次方程组可以有4组解相一致3。
赏析 阿尔哈岑的打弹子问题,在数学史上颇有影响,历史上曾有休金斯、巴诺、德.奥克塔勒、黎卡提和克特勒等著名数学家投入到这个问题的研究上来,这个问题的解决依赖于一个二次方程组的求解,较典型地把几何问题与代数问题揉合到一块了,解析几何的实际应用,这个问题是个例证。
从极值的角度来分析,阿尔哈岑弹子问题可以这样叙述:“在一个圆的圆周上找出一个点,使其与圆内两个已知点的距离之和最小(或最大)。”
阿尔哈岑曾对圆内两点和圆心距离相等的特殊性作过研究,他得出的结论是:已知圆和通过两已知点及已知圆圆心的圆的交点是已知圆上到这圆内两已知点距离之和最小的点。
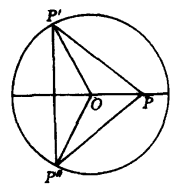
同时阿尔哈岑还研究了这样的问题:怎样去击一个圆台球桌上的弹子球,使其两次碰边缘后仍回到原位。如图4,P为弹子球的原位,撞击后,到P'点,P'点弹出至P”点,P”点再弹回到P,要达到这个目的,关键是要选准P'的位置3。
本词条内容贡献者为:
尹维龙 - 副教授 - 哈尔滨工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国