[科普中国]-嵌入下推自动机

嵌入下推自动机或 EPDA 是分析树-邻接文法(TAG)的计算模型。除了不再使用堆栈来存储符号之外，它类似于分析上下文无关文法的下推自动机。它有存储符号的重复堆栈组成的一个栈，这给予了 TAG 在上下文无关文法和上下文有关文法之间的复杂度，或者说是适度上下文有关文法的子集。

历史和应用EPDA 最初由 K. Vijay-Shanker 在他 1998 年的博士论文中描述。它们已经被应用于更完整的描述适度上下文有关文法类，并向乔姆斯基层级扩展和精细了这个文法类。各种子文法，比如线性附标文法可以从而定义。它们还在自然语言处理中扮演重要角色。

尽管自然语言有使用上下文无关文法来分析的传统(参见转换-生成语法和计算语言学)，但这个模型不适合有交叉依赖的语言如荷兰语，而 EPDA 就适合。详细的语言分析可见于引文。1

理论首先重申 EPDA 是有一组其自身可以通过“嵌入栈”来访问的栈的有限状态机，每个栈包含“栈字母表”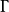 的元素，并且我们通过 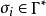定义一个栈的元素，这里的星号是字母表的Kleene闭包。

每个栈都可以依据它的元素来定义，所以我们使用双剑符号来指示在自动机中的第 个栈: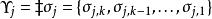 ，这里的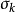 将是在栈中的下一个可访问的符号。 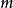个栈的“嵌入栈”因此可以指示为 。

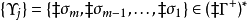我们定义 EPDA 为七元组：

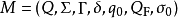这里的

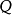是“状态”的有限集合；

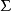是“输入字母表”的有限集合；

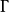是“栈字母表”的有限集合；

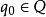是“开始状态”；

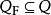只“最终状态”的集合；

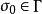是“初始栈符号”

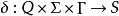是“转移函数”，这里的 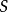是 的有限子集。

所以转移函数选取一个状态，输入字符串的下一个符号，和当前栈的顶符号；并生成下一个状态，在“嵌入栈”上要压入和弹出的那些栈，当前栈的压入和弹出，和要在下一个转移中被当作当前栈的栈。更加概念的说，“嵌入栈”是被压入和弹出的，当前栈被随意的压回到“嵌入栈”，而你希望的任何其他栈将被压入它的顶部，带有最后的栈是在下一个重复中所读取的。所以，这些栈被同时压入当前栈的上面和下面。

一个给定的格局被定义为

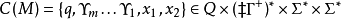
这里的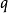 是当前状态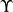，是在“嵌入栈”中的栈，带有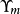是当前栈，而对于输入字符串 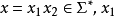是已经被机器处理的那部分字符串，而 是要处理的那部分，带有它的头部是当前所读的符号。注意空串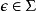被隐含的定义为终止符号，如果机器处于最终状态此时读到空串，则整个输入字符串被“接受”，如果不是则“拒绝”。这种“接受”了的字符串是如下语言的元素2

计算模型计算模型（computational model）是计算科学中的一个数学模型，它使用大量的计算资源来用计算机模拟研究一个复杂系统的行为。被研究的系统通常是一个复杂的非线性系统，这种系统不易取得简单、直观的解析解。相比于推导数学分析来解决问题，它是通过在计算机中调整系统参数并研究实验结果的差异来完成模型。模型的操作理论可以从这些实验来推断/推导。

常见的计算模型有天气预报模型、地球模拟器模型、飞行模拟器模型、分子蛋白质折叠模型和神经网络模型。2

上下文有关文法上下文有关文法(CSG，英语：context-sensitive grammar)是一种形式文法，其中任何产生式规则的左手端和右手端都可以被终结符和非终结符构成的上下文所围绕。上下文有关文法比上下文无关文法更一般性，但仍足够有秩序得可以被线性有界自动机所解析。

上下文有关文法的概念是诺姆·乔姆斯基在1950年代介入的，被作为描述自然语言的语法的一种方式，在自然语言中一个单词是否可以出现在特定位置上，要依赖于上下文。可以被上下文有关文法描述的形式语言叫做上下文有关语言。1

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所