[科普中国]-反三角方程

反三角方程(inverse trigonometric equation)一类特殊方程。指在反三角函数记号后含有未知数的方程(一般只讨论单值反三角函数方程)，反三角方程多数不能用初等方法求解，能用初等方法求解的仅限于一些简单的反三角方程。其解法通常是将方程两边同取某一三角函数，使之化成代数方程来求解，由于反三角函数有值域的限制，所以，反三角方程两边的角应属同一区间，否则这样的反三角方程无解。解反三角方程时，在方程变形的过程中，若使用了非同解变形的方法，就有可能增根或失根，所以都要验根1。

定义未知数含有反三角函数符号的方程，我们叫做反三角方程。例如2arcsin x=arcsin 10x/13，(arccos x)²-6arccos x+8=0等都是反三角方程。

最简的反三角方程最简的反三角方程如arc sin x=θ，arc cos x=θ，arc tg x=θ，arc ctg x=θ。

解反三角方程的目的是要求出未知数，使得它能满足方程所给出的反函数值。

上面四个反三角函数，它们的取值范围为-π/2≤arc sin x≤π/2，0≤arc cos x≤π，-π/2﹤arc tg x﹤π/2，0﹤arc ctg x﹤π。

所以，反三角方程不一定有解2。

其他反三角方程解反三角方程的根本方法是把方程两边同取某一三角函数的三角运算，使它转化为代数方程，按代数方程的解法来解。但是应该指出，两边取三角运算所得的方程与原方程不一定是同解方程，会有增根产生的可能性，必须进行根的检验，去伪存真3。

例 解方程

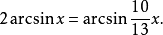解 在原方程两边取正弦得

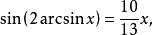即

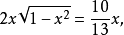
解之， 得

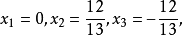经检验 x=0是原方程的根。

因为

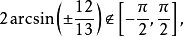而

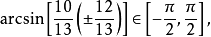所以 x2，x3都是增根3。

解三角方程与反三角方程的技能解三角方程与反三角方程的技能指以最简三角方程的通解为基础，利用解代数方程的知识：三角式的恒等变形和换元法等，求得三角方程和反三角方程解集的技能4。

解三角方程与反三角方程技能训练的基本要求是：①熟练掌握最简三角方程的通解。②善于观察所给方程的特点，熟练把握恰当的解题思路。如果一个三角方程可化为只含有一个未知数的同一个三角函数的方程，则用换元法转化为解代数方程，求得这个三角函数的值，再解所得最简三角方程。如果一个三角方程可化为两个同名函数相等的形式，则利用相等的充要条件来解。sinf(x)= sing(x)的充要条件为f(x)=nx+(-1)ng(x),cosf(x)= cosg(x)的充要条件为f(x)=2nπ±g(x),tgf(x)= tgg(x)的充要条件为f(x)=nπ+g(x)(以上n为整数)。如果一个三角方程可化为一边是零，另一边可分解因式，则转化为几个较简单的三角方程来解，但要知道，使某一个因式为零的值，必须使其它几个因式均有意义，否则即为增根，要舍去。③掌握关于sinx和cosx的齐次方程求解的一般步骤；先化为只有tgx的方程，用代数方法求出tgx的值，再求x。如果一个三角方程中常数项不为零，而其它项关于sinx与cosx是齐次的，常可能过1= sin²x+cos²x的代换，把该方程化为齐次方程。④掌握形如asinx +bcosx=c(a≠0,b≠0)的方程的解法：一般引入辅助角，将原方程变形为， (其中φ是已知数，由确定)来解。这样得到的新方程与原方程是同解的。⑤掌握形如f(sinx,cosx,tgx,ctgx)=0的方程(左端是sinx ,cosx,tgx,ctgx的有理式,某些三角函数也可以不出现)的解法:可以用“万能代换”来解。即令，于是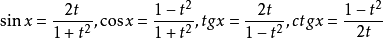，原方程化内t的有理方程F(t)=0，用代数法解出t，再得x。需要知道的是，代换后的新方程要求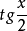有意义，即x≠(2k+1)π(k为整数),而原方程中如果ctgx不出现，这些值也有可能是原方程的解。因此，利用万能代换解三角方程时，必须检查(2k+1)π是否是原方程的解，防止失根4。

应当注意的是：①解三角方程时，由于方程变形可能破坏同解性，进行三角变换可扩大或缩小定义域，常会发生增根、失根；又会因解法不同或选用的辅助函数不同使增根、失根出现不同的情况，因此必须尽可能避免增根、失根，当无法避免时,要剔除增根，找回失根。由于三角方程的解集一般是无限集较好的方法是利用方程的周期(把周期函数f(x)的周期也叫做方程f(x)=0的周期)来验根，只需先求出方程的周期，在一个周期内进行验根，即可得出一般结论。凡原方程中有tgx,secx等函数时，应注意有没有增根x=kπ+π/2；有ctgx，cscx等函数时应注意有没有增根x=kx。原方程中不含这类函数，而变形后的方程却有这类函数时，要注意检查这些值是不是原方程的根，防止失根。②三角方程的解集一般是无限集，而三角函数是周期函数，可解集可用通解公式表示。但常因在解的过程中所用公式不同，或选取的特殊角的代表值不同，而使得同一个三角方程的通解公式会有不同的形式。如果已经剔除增根，找出失根，那么不同形式的解集应相等。检查这一点，通常可以在三角方程的一个周期内把不同形式的解所表示的角的终边位置进行比较。

对于仅在反三角函数符号后面含有未知数的反三角方程，一般将其两端施以同一个三角运算，得到一个代数方程，然后求解。在此解法过程中，往往会破坏同解性。如反三角方程f(x)=g(x)与方程sinf(x) = sing(x)及方程cosf(x) = cosg(x)都不同解，但都只有增根的可能，不会失根，而反三角方程f(x)=g(x)与方程tgf(x)=tgg(x)也不同解，既可能有增根，又可能失根。所以应根据方程特点进行检查4。

本词条内容贡献者为:

方正 - 副教授 - 江南大学