[科普中国]-样本分位数峰度

样本分位数峰度(sample quantile kurtosis)是指将分位数峰度中的分位数换成相应的样本分位数所得的统计量。分位数峰度是由四分位数和十分位数构造的，单峰分布曲线的“峰”之陡峭程度的一种度量。

基本介绍设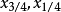 和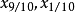 相应为随机变量X的上、下四分位数和上、下十分位数，则称

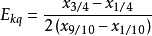为X的分位数峰度。对于正态分布， 。

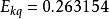峰度及测度在社会经济现象中，许多变量数列的曲线与正态分布的曲线相比，其顶部的形态会有所不同，即分布图形的尖峭程度或扁平程度有所不同。如果一个总体在众数周围集中的程度很高，其分布的图形就会比较陡峭；反之，如果总体在众数周围的集中程度较低，其分布的图形就会比较平坦。峰度指标就是反映这方面的分布情况的一个数值特征1。

样本峰度对于具有n个值的样本，样本峰度2为：

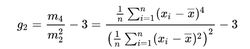
其中m4是四阶样本中心矩，m2是二阶中心矩（样本方差），xi是第i个值，X bar是样本平均值。注意此处计算方差的时候除数是N，而不是单独计算样本方差的(N-1)。

另有公式：

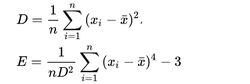
其中，n为样本大小，D为事先计算的方差，xi是第i个值，X bar是样本算术平均值。

在统计软件如Excel中，计算样本的峰度公式如下：

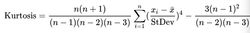
矩法在一般情况下，总体分布图形的陡峭程度与偶数阶中心矩的数值大小有关。如偶数阶中心矩的数值越大，分布图形越平坦；数值越小，分布图形越尖峭。如果将分布的四阶中心矩与标准差的四次方对比，得到的数值大小与峰度的高低能够保持一致，同时又恰好消除了计量单位对计算结果的影响。由此形成了峰度指标的基本构造方式。但对于正态分布，这样计算的结果恒为一个常数：

因此，可以将各种分布的峰凸程度都与正态分布相比，得到峰度的标准测定公式：

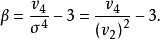按照上面公式计算出来的峰度指标，可以用来判定分布的形态特征。其判定标准为：

当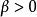 时，分布为高峰度

当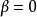 时，分布为正态分布

当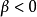 时，分布为低峰度

这里所说的峰度高、低，都是与具有相同标准差或方差的正态分布比较而言的1。

分位数法为了排除极端值的干扰，分布的峰度也可以采用分位数的方法来测定。例如，人们常利用上、下两个四分位数和上、下两个十分位数之间的数量关系来衡量峰度：

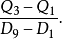
观察表明，计算得到的数值越小，分布图形越陡峭；反之，数值越大，分布图形越平坦。理论上可以证明，对于正态分布，这样计算的结果总是0.526，故可以定义相应的“分位数峰度”指标为

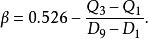该指标的判别标准与矩法给出的峰度指标基本相同1。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学